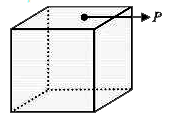
A solid cube is placed on a horizontal surface. The coefficient of friction between them is . A variable horizontal force is applied on the cube’s upper face, perpendicular to one edge and passing through the mid-point of edge, as shown in figure. The maximum acceleration with which it can move without toppling is (take )
1
5
4
None of the Above
The correct Answer is:B
hence
Similar Questions
A body of mass 25 kg, is placed on a horizontal surface whose coefficient of friction 0.25. Find the frictional force action on it. Take (g=10ms−2)
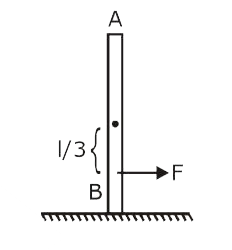
View SolutionA uniform rod ABC of mass M is placed vertically on a rough horizontal surface. The coefficient of kinetic friction between the rod and the surface is μ.A force F (>μmg) is applied on the rod at point B at distance l/3 below centre of the rod as shown in figure. The initial acceleration of point A is
View Solution
Knowledge Check
In the figure, a solid uniform cube is placed on a horizontal surface. The co-efficient of friction between them is μ where μ<12. A variable horizontal force perpendicular to one edge and passing through the midnight of that applied on the cube's upper face. The maximum acceleration with which it can move without toppling is
 AμgBg(1−2μ)2Cg(1−2μ)D(μ+12)g
AμgBg(1−2μ)2Cg(1−2μ)D(μ+12)gA block of mass m is placed on a horizontal surface. The coefficient of frication between them is μ. The block has to be moved by applying a single external force on it. The force may be applied in my direciton. The minimum value of this force must be
Amg, applied vertically upward, if μ>1Bμmg, applied horizontally, if μ<1Cμmg√μ2+1 for all values of μDμ2mgμ2+1 for all values of μA body of mass 2 kg is placed on a horizontal surface having coefficient of kinetic friction 0.4 and limiting coefficient of static friction 0.5. If a horizontal force 2.5 N is applied on the body, the frictional force acting on the body will be (Take, g=10ms2)
A8 NB10 NC20 ND2.5 N
A 4 kg block is placed on a rough horizontal surface. The coefficient of friction between the block and the surface is μ=0.5. A force F = 18 N is applied on the block making an angle θ with the horizontal. Find the range of values of θ for which the block can start moving.
[Take g=10m/s2,tan−1(2)=63∘sin−1(109√1.25)=84∘]
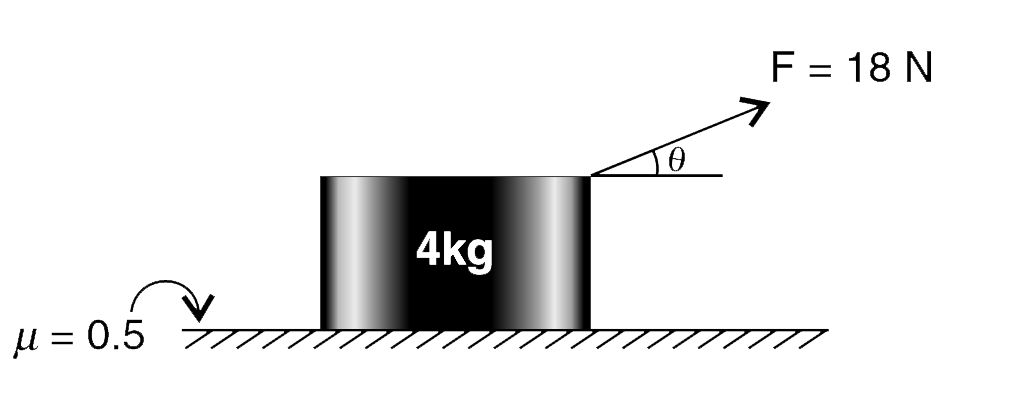
View SolutionA block of mass 1 kg start moving at t = 0 with speed 2m/s on rough horizontal surface with coefficient of friction 0.2. A horizontal force F is applied in the direction of velocity which varies with time as shown in figure. Find the speed (in m/s) of particle at t = 3 s.

View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
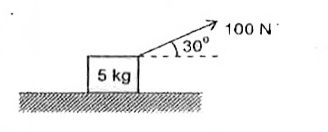
View SolutionA block of mass 5 kg is placed on a rough horizontal plane. The coefficient of static and kinetic friction between the block and surface is 0.5 and 0.3 respectively. A force of 100 N is applied at an angle of 30∘ from the horizontal as shown in the figure. The acceleration of the block will be [g=10m/s2]
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View Solution
