Question

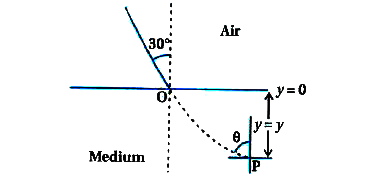
As shown in figure a ray of light in air is incident at ${30}^{\circ }$ on a medium and proceeds ahead in the medium. The refractive index of this medium varied with distance y as given by
$n\left(y\right)=1.6+\frac{0.2}{{(y+1)}^2}$ where y is in cm. What is the angle formed by the ray with the normal at a very large depth ?

Explanation

`rArr` Suppose the angle is `theta` at distance in the medium.
Appyling Snell.s law at this point,
`n(y) sin theta= C,` where C = constant ....... (1)
This formula is ture for all the pionts,
Applying it to poin O,
`n(0) sin 30^@ = C`
But, `n(0) = 1.6 + (0.2)/((0+1))^2`
`therefore n(0) = 1.8 `
From equation (2),
`therefore n(0) = 1.8 xx 1/2 =C`
`therefore 0.9 = C`
Puting this value in (1), n(y) sin `theta` = 0.9
`therefore {1.6 + (0.2)/((y+1)^2)} sin theta =0.9`
`therefore sin theta= (0.9)/(1.6 + (0.2)/(y+1)^2)`
When y is very large, taking `y rarr oo`,
we get sin `theta = (0.9)/(1.6)`
`therefore theta = 34^@ 14.`