A disc of radius R is rotating with an angular ω0 about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is μk.
(a) What was the velocity of its centre of mass before being brought in contact with the table?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table?
(c) What happens to the linear speed of the centre of mass when disc is placed in contact with the table?
(d) Which force is responsible for the effects in (b) and (c )?
(e) What condition should be satisfied for rolling to being?
(f) Calculate the time taken for the rolling to begin. Solution in Gujrati
(a) The disc was in pure rotational motion before being brought in contact with the table, hence uCM=0
(b) Velocity of a point on the rim decreases when the disc is placed in contact with the table due to friction.
(c ) Centre of mass acquires some linear velocity when the rotating disc is placed in contact with the table due to friction.
(d) Friction is responsible.
(e) When rolling starts vCM=ωR.
(f) Acceleration produced in centre of mass due to friction.
aCM=fm=μKNm=μKmgm=μKg
Angular retardation produced by the torque due to friction.
α=τI=μKmgRI [∵τ=fR=μKmgR]
∴vCM=uCM+aCMt(∵uCM=0)
∴vCM=μKgt
Now ω=ω0+αt
∴ω=ω0−μKmgRIt
For rolling without slipping,
vCMR=ω
∴vCMR=ω0−μKmgRlt
μKgtR=ω0−μKmgRlt
t=Rω0μKg(1+mR2l)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-E MULTIPLE CHOICE QUESTIONS
Explore 105 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-F QUESTIONS FROM MODULE
Explore 22 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-D NCERT EXEMPLAR SOLUTIONS (SHORT ANSWER TYPE QUESTIONS)
Explore 4 Videos
- QUESTIONS ASKED IN JEE - 2020 Book:KUMAR PRAKASHANChapter:QUESTIONS ASKED IN JEE - 2020 Exercise:Question
Explore 16 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
Explore 1 Video
Similar Questions
Peak value divided by the rms value gives us
View SolutionIf I1 is the moment of inertia of a uniform rod about an axis perpendicular to its length and passing through its one end. Now ring formed by bending the rod, if the moment of inertia about the diameter of ring I1 then I1I2 = ……….
View SolutionThe vector sum of a system of non-collinear forces acting on a rigid body is given to be non-zero. If the vector sum of all the torques due to the system of forces about a certain point is found to be zero, does this mean that it is necessarily zero about any arbitrary point?
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionA disc roating about its axis with angular speed omega_(0) is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R . What are the linear velocities of the points A, B and C on the disc shown in Fig. Will the disc roll in the direction indicated ?
View SolutionA disc of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is μk.
(a) What was the velocity of its centre of mass before being brought in contact with the table ?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) What happens to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) Which force i sresponsible for the effects in (b) and (c ).
(e) What condition should be satisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin.
View SolutionA disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.
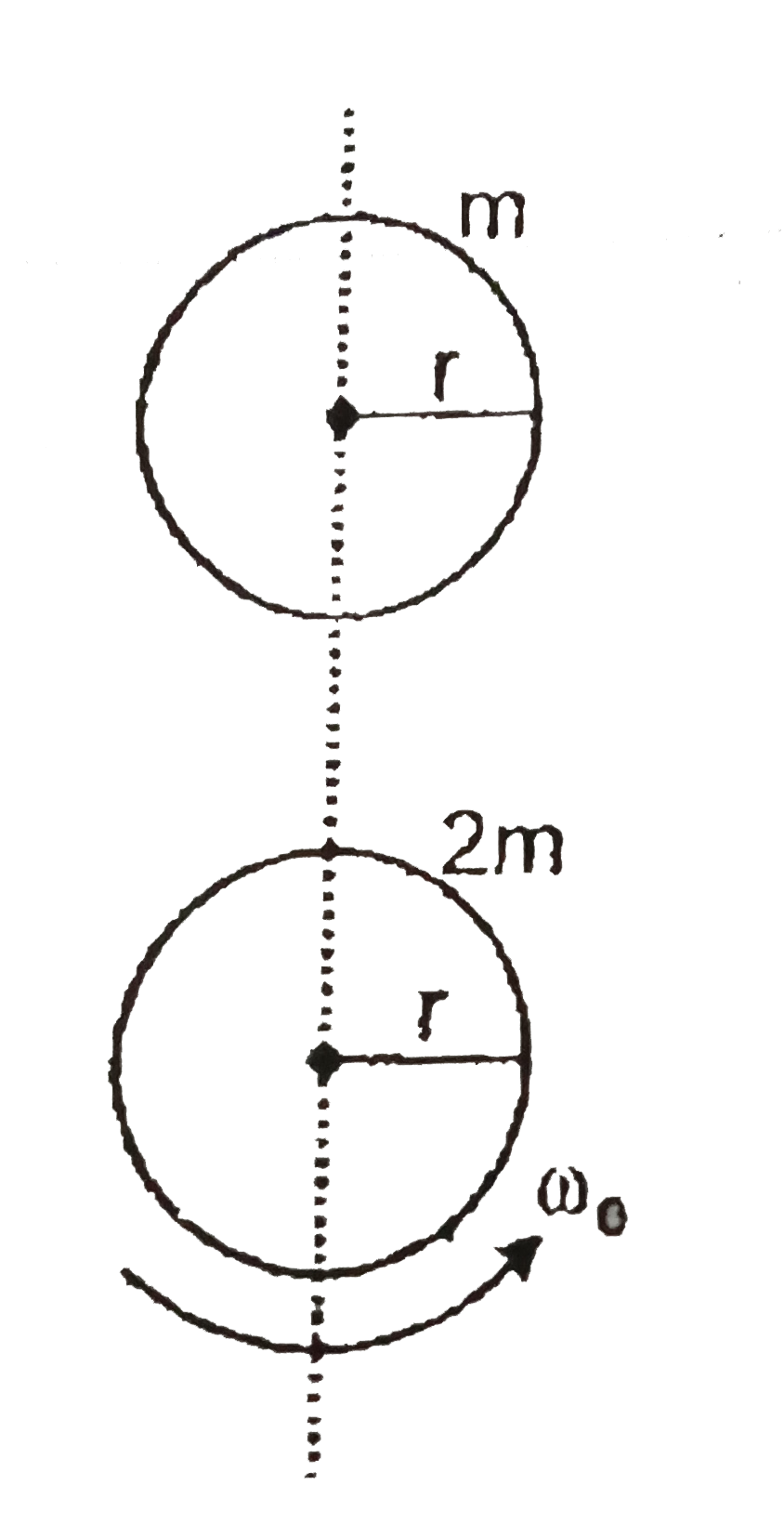
Time elapsed in this process
View Solutionअपने अक्ष पर ω0 कोणीय चाल से घूर्णन करने वाली किसी चक्रिका को धीरे से ( स्थानांतरीय धक्का दिए बिना ) किसी पूर्णतः घर्षणरहित मेज पर रखा जाता है । चक्रिका की त्रिज्या r है । चित्र में दर्शाई चक्रिका के बिंदुओं A, B तथा C पर रैखिक वेग क्या हैं ? क्या यह चक्रिका चित्र में दर्शाई दिशा में लोटनिक गति करेगी ?

View SolutionA disc rotating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?
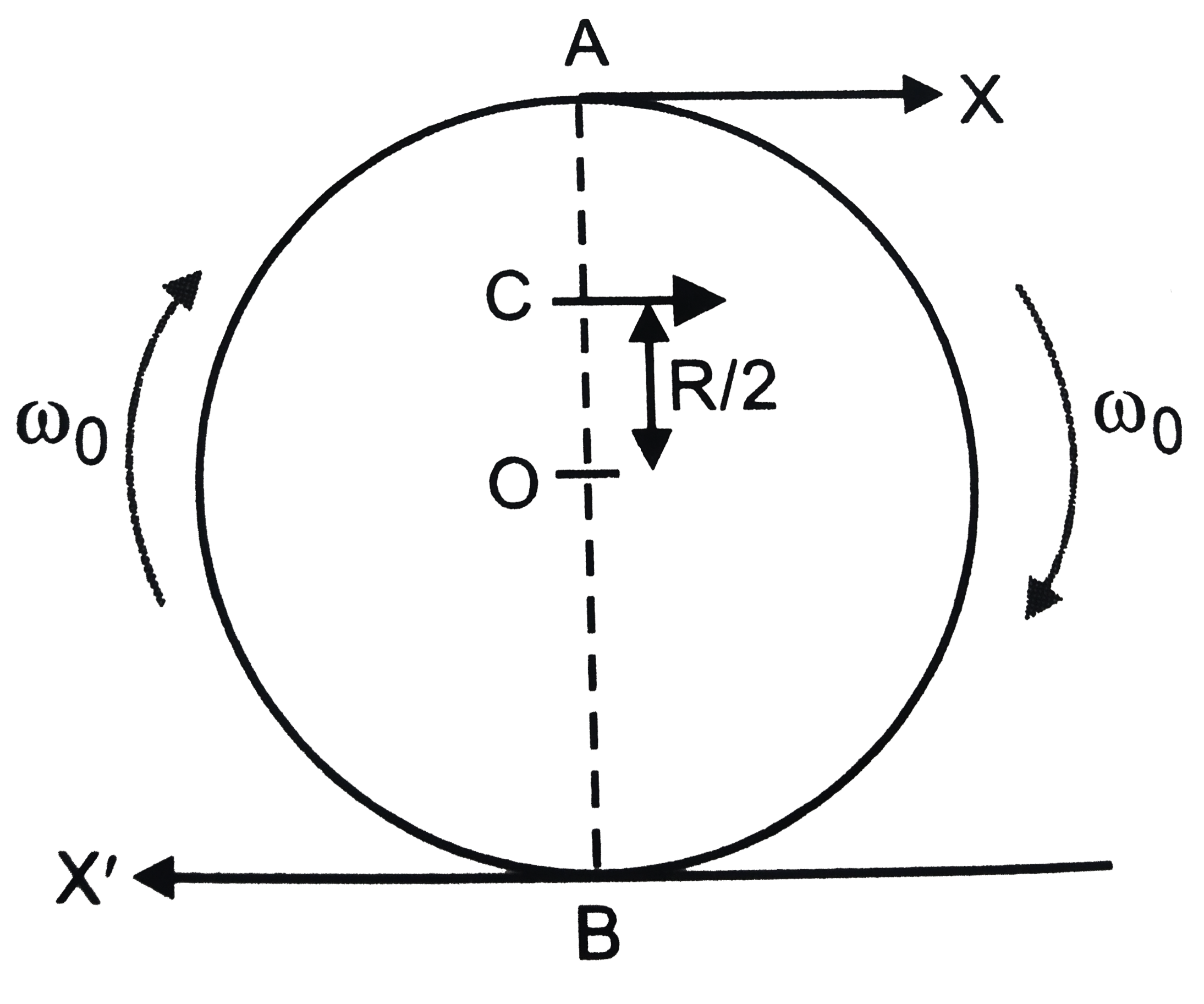
View SolutionA disc rotating about its axis with angular speed omega_(0) is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R . What are the linear velocities of the points A, B and C on the disc shown in Fig. Will the disc roll in the direction indicated ?
View Solutionकिसी घूमने वाली क्षैतिज मेज पर रखी कोई छोटी-सी वस्तु ठीक उस समय फिसल जाती है जब उसे घूर्णन अक्ष से 4 सेमी की दूरी पर रखा जाता है। यदि उस घूमने वाली मेज के कोणीय वेग को दुगुना कर दिया जाए, तो वह वस्तु उस समय फिसलती है जब घूर्णन अक्ष से उसकी दूरी होती है -
View SolutionR त्रिज्या की वलय क्षैतिज अक्ष के परितः कोणीय चाल ω0 से घूर्णन कर रही है। इसे खुरदरे क्षैतिज मेज पर रखा जाता है। गतिज घर्षण गुणांक μk है। वह समय क्या होता है जिसके पश्चात् यह लुढ़कना शुरू करती है?
View SolutionA disc of radius R is rotating with an angular omega_(0) about a horizontal axis it is placed on a horizontal table . The coefficient of kinetic friction is mu _(k) (a) what was the velocity of its centre of mass before being brought in contact with a the table ? (B) what happens to the linear velocity of a point on its rim when placed in contact with the table ? (c ) what happes to the linear speed of the centre of mass when disc is placed in contact with the table ? (d) which force is responsible for the effects in (b) and (C ) ? (e) wht condition should be sattisfied for rolling to begin ? (f) Calculate the time taken for the rolling to begin .
View SolutionA circular disc rotates freely about a vertical axis through its centre with angular velocity ω1. A ring having the same mass and radius as the disc is placed on the disc and the system now rotates with an angular velocity ω2 about the same vertical axis. Then ω2/ω1 is:
View Solution

