Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken. Solution in Gujrati
Suppose each particle of mass m is moving along two parallel lines at distance d.
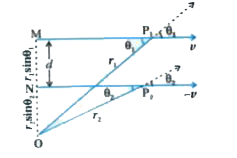
Each particle has speed v in opposite direction. Suppose at any instant particles are at point P1andP2.
Suppose the angular moment of both particle with respect to point O is −→L1and−→L2.
∴−→L1=→r1×m→v=and−→L2=→r2×m→v
Now suppose the angular momentum of the system is →L
∴→L=−→L1−−→L2
=→r1×m→v−→r2×m→v
Negative sign is present due to both particle moves in opposite direction
∴∣∣→L∣∣=∣∣∣−→L1∣∣∣−∣∣∣−→L2∣∣∣
=mvr1sinθ1−mvr2sinθ2
=mv[r1sinθ1−r2sinθ2∣....(1)
where θ1 angle is between →r1and→vandθ2 angle is between →r2and→v
∴OM=r1sinθ1andON=r2sinθ2 and OM−ON=d
r1sinθ1−r2sinθ2=d
∴ From eqn. (1)
L=mvd
Direction L is perpendicular to the plane form by →rand→v and it toward inside end does not change it direction with line and hence the magnitude and direction of angular momentum remains constant, so L is unchanged.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-B ADDITIONAL EXERCISE
Explore 12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-B NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK
Explore 17 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-B NUMERICALS
Explore 29 Videos
- QUESTIONS ASKED IN JEE - 2020 Book:KUMAR PRAKASHANChapter:QUESTIONS ASKED IN JEE - 2020 Exercise:Question
Explore 16 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
Explore 1 Video
Similar Questions
The longest wavelength in Balmer series of hydrogen spectrum will be
View SolutionThe particles of mass m1,m2andm3 are placed on the vertices of an equilateral triangle of sides .a.. Find the centre of mass of this system with respect to the position of particle of mass m1.

View SolutionFind the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
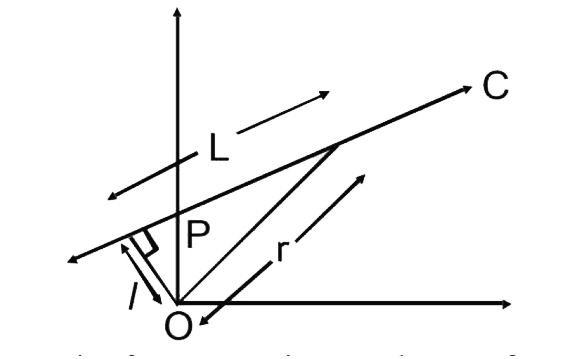
View SolutionTwo particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
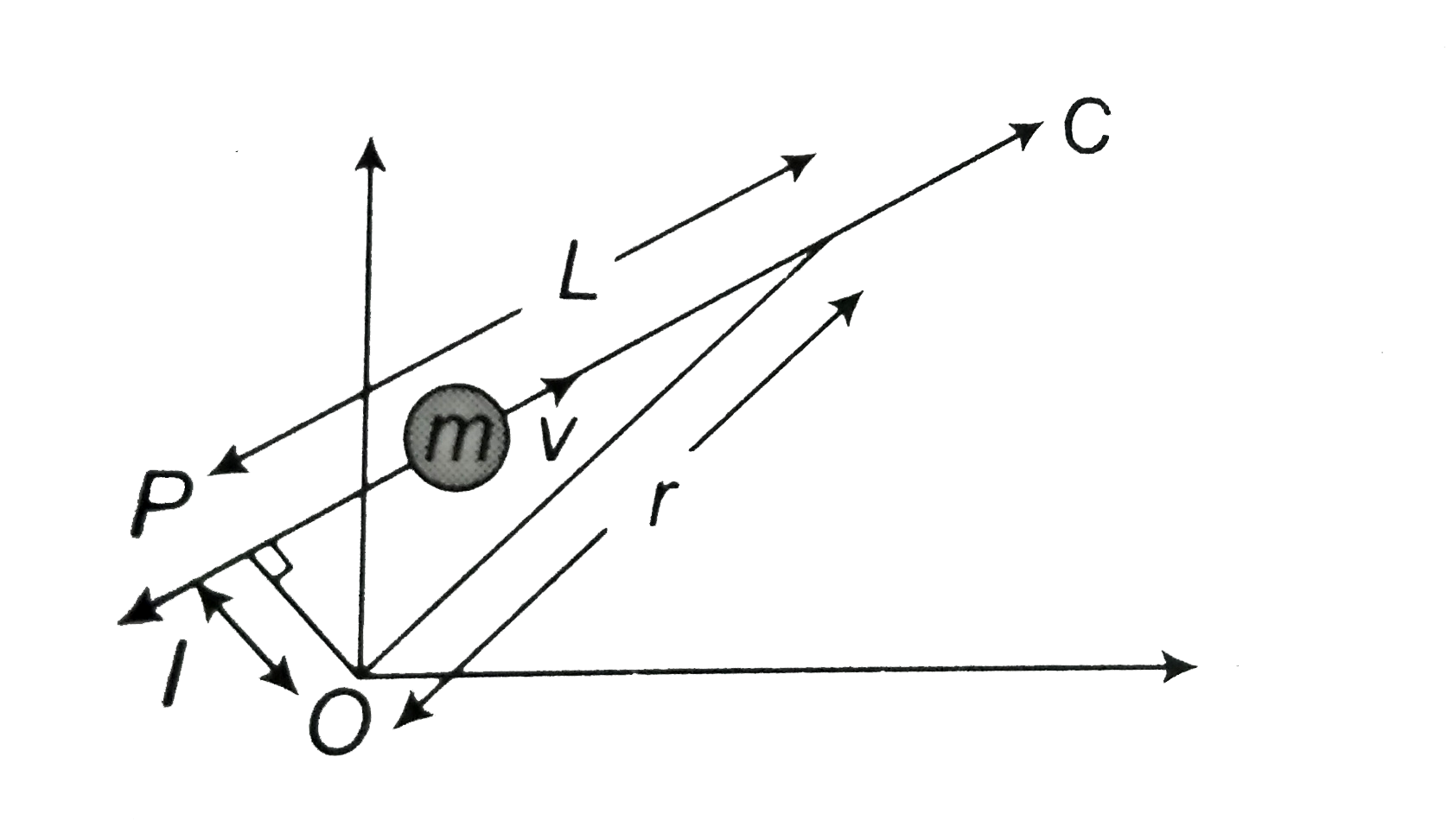
View SolutionA particle P collides elastically at M with a speed v . The change in angular momentum the particle about the point N during collision is
View Solutionदो कण जिनमे से प्रत्येक का द्रव्यमान m एवं चाल है d दूरी पर , समान्तर रेखाओ के अनुदिश , विपरीत दिशाओ में चल रहे है । दर्शाइये कि इस द्विकण निकाय का संदिश कोणीय संवेग समान रहता है , चाहे हम जिस बिंदु के परित : कोणीय संवेग ले ।
View Solutionदो कण जिनमें से प्रत्येक का द्रव्यमान m एवं चाल v है d दूरी पर, समान्तर रेखाओं के अनुदिश, विपरीत दिशाओं में चल रहे हैं। दर्शाइए कि इस द्विकण निकाय का सदिश कोणीय संवेग समान रहता है, चाहे हम जिस बिन्दु के परितः कोणीय संवेग लें।
View SolutionA particle of mass m travels with speed v along + ve direction of x-axis parallel to line y=6 . At t=0 , the particle is at (0, 6). The angular momentum of particle about origin is :
View Solutionm ভরের একটি কণা x- অক্ষের সমান্তরাল একটি রেখা বরাবর সমবেগে যাছে । মূলবিন্দুর সাপেক্ষে কণাটির কৌণিক ভরবেগ
View SolutionTwo particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View Solutionm द्रव्यमान का एक कण PC रेखा के अनुदिश (चित्रानुसार) v वेग से गति करता है। बिन्दु O के परितः कण का कोणीय संवेग
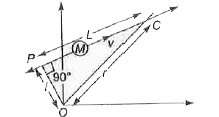
View Solutionदो कण जिनमें प्रत्येक का द्रव्यमान m तथा चाल है, समान्तर रेखा पर अलग-अलग विपरीत दिशा में d दूरी से गति कर रहे हैं। दोनों कणों का कोणीय संवेग है
View Solution