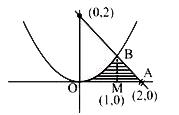
The area bounded by the curves $x + y = 2$ and $y = x^{2}$ above x-axis in the first quadrant is ,

$\frac{1}{2}$

$\frac{2}{3}$

$\frac{10}{12}$

$\frac{6}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

The area bounded by the curves $y = x^{2} and y = 2 - x^{2}$ is
A $\frac{8}{3}$ sq units
B $3 / 8$ sq units
C $3 \frac{/}{2}$ sq units
DNone of these
The area bounded by the curves y = |2 - 2'| and y = x + 3 and the y-axis in the first quadrant
A $\frac{31}{2} + \frac{5}{I n 2}$
B $\frac{31}{2} - \frac{5}{I n 2}$
C $\frac{5}{I n 2} - \frac{1}{2}$
D $\frac{1}{2} + \frac{5}{I n 2}$
The area (in sq. units) of the region bounded by the curves $y = 2^{x}$ and $y = | x + 1 |$ , in the first quadrant is :
A $\frac{3}{2} - \frac{1}{{log}_{e} 2}$
B ${log}_{e} 2 + \frac{3}{2}$
C $\frac{3}{2}$
D $\frac{1}{2}$