F1andF2 are the two foci of the ellipse x29+y24=1. Let P be a point on the ellipse such that |PF1|=2|PF2|, where F1andF2 are the two foci of the ellipse . The area of △PF1F2 is :
A
3
B
4
C
√5
D
√132
Video Solution
Text Solution
The correct Answer is:B
Given |PF1|=2|PF2|
Also, |PF1|+|PF2|=6⇒|PF2|=2and|PF1|=4
Also b2=a2(1−e2)⇒4=a(1−a2)
⇒e=√53⇒F1F2=2√5
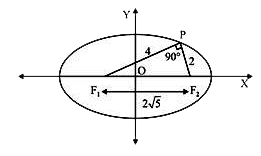
Now PF21+PF22=(F1F2)2⇒∠P=90∘
So , area (ΔPF1F2)=12(4×2)=4
|
Similar Questions
Knowledge Check
Foci of ellipse (x−1)24+(y−2)29=1 is/are
A(1,2)+√5)B(1,2−√3)C(1+2√53,2)D(1−2√53,2)The coordinates of the foci of the ellipse x216+y29=1 will be-
A(0,±√21)B(0±5)C(±√7,0)DNone of theseThe coordinates of the foci of the ellipse x249+y236=1 will be-
A(0,±√75)B(±√13,0)C(0,±√15)DNone of these
The distance from the foci of P(a,b) on the ellipse x29+y225=1 are
View SolutionLet F1,F2 be two foci of the ellipse x2p2+2+y2p2+4=1 . Let P be any point on the ellipse , the maximum possible value of PF1.PF2−p2 is
View SolutionThe coordinates of the foci of the ellipse x2A+y225=1 will be-
View SolutionThe coordinate of foci of the ellipse x225+y29=1 is
View SolutionConsider an ellipse x213+y24=1 and a variaote point P(1-,2t) is takne in such a way that ∠S1PS2 is maximum where S1andS2 are the foci of the given ellipse then the value of S1PS2P is
View Solution
