From a circle of radius a, an isosceles right angled triangle with the hypotenuse as the diameter of circle is removed. The distance of the centre of gravity of the remaining portion from the centre of the circle is : Solution in Telugu
3(π−1)a
(π−1)a6
a3(π−1)
a3(π+1)
The correct Answer is:C
Step by step video, text & image solution for From a circle of radius a, an isosceles right angled triangle with the hypotenuse as the diameter of circle is removed. The distance of the centre of gravity of the remaining portion from the centre of the circle is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - I) LEVEL - I
7 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - PRACTICE SHEET (EXERCISE - I) LEVEL - II
1 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - LECTURE SHEET (EXERCISE - II)
4 Videos
- CALORIMETRY BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)
1 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
Three particle each of 1 kg mass are placed at corners of a right angled triangle AOB, 'O' being the origin of coordinate system (OA and OB along the x-direction and +ve y-direction). If OA = OB = 1m, the position vector of centre of mass (in metres) is
View SolutionA rope thrown over a pulley has ladder (of mass M - m) with a man of mass m on one of its ends and a counterbalancing mass M on its other end The man climbs with a velocity vr relative to a ladder. Pulley and rope are ideal. The velocity of centre of mass of the system is
View SolutionThe centre of mass of a non uniform rod of length L whose mass per unit length λ=Kx2L, where L is a constant and x is the distance from one end is
View SolutionThree liquids A,B and C having same specific heat and mass m , 2m and 3m have temperature 20∘C,40∘Cand60∘C respectively. Temperature of the mixture when :
Column -IColumn -IIA) A and B are mixed,is atP)35∘CB) A and C are mixed , is at Q)52∘CC) B and C are mixed , is at Q)50∘CD) A , B and C all three are mixed , is at S)45∘CT) None
View SolutionFour identical balls A,B,C and D are placed in a line on a frictionless horizontal surface. A and D are moved with same speed .u. towards the middle as shown. Assuming elastic collisions, find the final velocities.
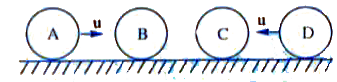
View SolutionFrom each of the two opposite corners of a square of side 8cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of diameter 4.2cm is also cut from the centre as shown in figure. Find the area of the remaining (shaded) portion of the square.
View SolutionA right angled isosceles triangle is inscribed in a semi-circle of radius 7cm. The area enclosed by the semi-circle but exterior to the triangle is:
View SolutionFrom a circle of radius a, an isosceles right angles triangle with the hypotenuse as the diameter of the circle is removed. The distance of the centre of mass of the remaining portion from the centre of the circle is
View SolutionThe isosceles triangle ABC is inscribed in a circle with centre at O. If AP is a diameter of the circle. Then prove that AP is the bisetors of ∠BPC.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionIf angle between two tangent from point at distance 10 cm from centre of circle is 60^@ then radius of circle is
View SolutionIf triangle is inscibe in circle such that each side is equidistant from the centre of a circle then triangle is
View SolutionThe distance from the centre of a circle to the circumference is that of a diameter.
View SolutionLet ‘O’ be the centre of a circle, PQ is a diameter, then prove that ∠PRQ=90∘ (OR) Prove that angle in a semi-circle is right angle.
View SolutionLet ‘O’ be the centre of a circle, PQ is a diameter, then prove that angle PRQ = 90^@ (OR) Prove that angle in a semi-circle is right angle.
View Solution
