If the resultant of any two vectors →Aand→B is numerically equal to the either vector, the angle between the vectors can be:
cos−1(−B2A)andcos−1(−A2B)
sin−1(AB)andcos−1(−B2A)
sin−1(−AB)andcos−1(−2AB)
none of these
The correct Answer is:A
Topper's Solved these Questions
- VECTORSBook:AAKASH SERIESChapter:VECTORSExercise:Practice Sheet (Exercise-II) (Resolution of Vectors (Level -I)) (Straight Objective Type Questions)
Explore 19 Videos
- VECTORSBook:AAKASH SERIESChapter:VECTORSExercise:Practice Sheet (Exercise-II) (Resolution of Vectors (Level -II)) (Straight Objective Type Questions)
Explore 8 Videos
- VECTORSBook:AAKASH SERIESChapter:VECTORSExercise:Practice Sheet (Exercise-I) (Addition of Vectors) (Level-I) (Straight Objective Type Questions)
Explore 17 Videos
- UNITS AND MEASUREMENTS Book:AAKASH SERIESChapter:UNITS AND MEASUREMENTS Exercise:ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
Explore 14 Videos
- VISCOSITY Book:AAKASH SERIESChapter:VISCOSITY Exercise:Questions for Descriptive Answers
Explore 3 Videos
Similar Questions
Knowledge Check
If the angle between two vectors →a and →b is zero, then :
A→a.→b=|→a|∣∣→b∣∣B→a.→b=0C|→a|∣∣→b∣∣=1DNone of the aboveMagnitude of resultant of two vector →A and →B is equal to 2. angle between two vectors is 180∘ if ∣∣→A∣∣=3 then find ∣∣→B∣∣
A5B3C1D4The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
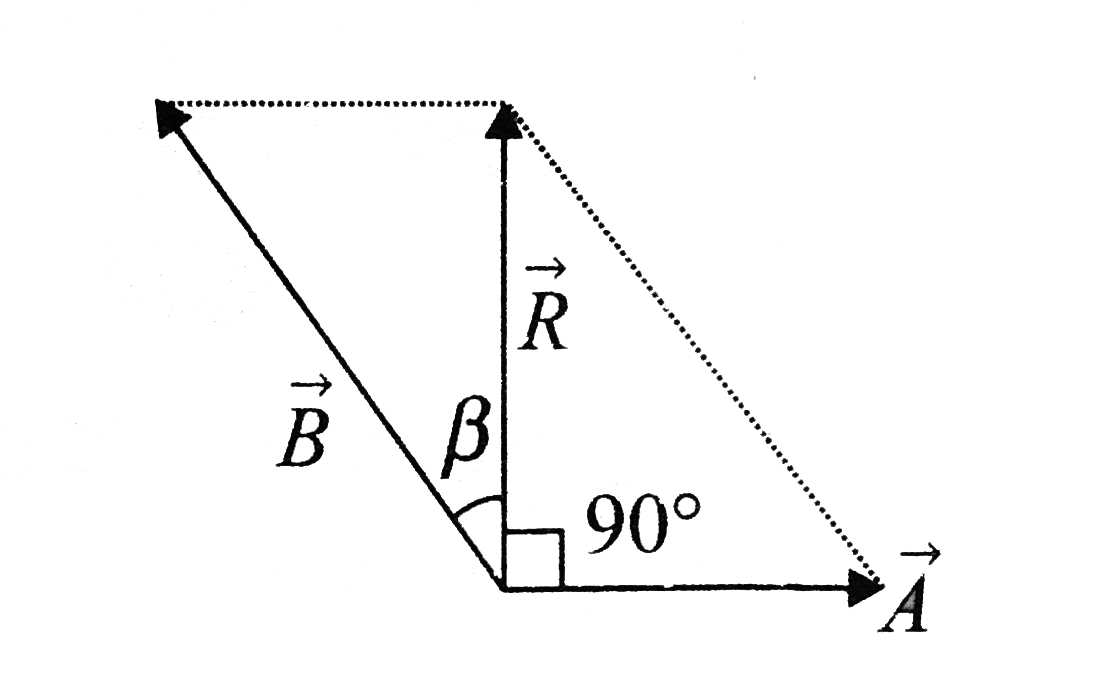 A120∘B150∘C135∘DNone of these
A120∘B150∘C135∘DNone of these
The resultant and dot product of two vectors →aand→b is equal to the magnitude of →a. Show that when the vector →a is doubled , the new resultant is perpendicular to →b .
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is

View SolutionIf for two vectors →A and →B,→A×→B=0, the vectors
View SolutionThe resultant of two vectors →Aand→B is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. What is the angle between →Aand→B ?
View SolutionThe cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
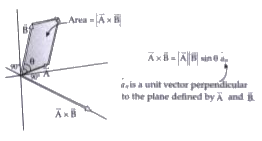
The angle between →a×→b and →b×→a is ___________.
View Solution

