A hydrogen-like atom (atomic number Z) is in a higher excited state of quantum number n. This excited atom can make a transition to the first excited state by successively emitting two photons of energies 10.20 eV and 17.00 eV respectively. Alternatively the atom from the same excited state can make a transition to the second excited state by snccessively emitting two photons of energies 4.25 eV and 5.95 eV respectively. Determine the values of n and Z (ionization energy of hydrogen atom = 13.6 eV) Solution in Telugu
n=5
z=2
n=6
z=3
The correct Answer is:C, D
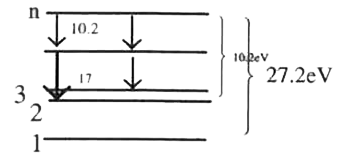
E=−22n2(13.6eV)
⇒R.hc.z2(19−1n2)=27.2…..(1)
⇒R.hc.z2(19−1n2)=10.2eV…(2)
(1)(2)=(n2−44n2)(n2−99n2)=27.210.2=2.66
9(n2−4)×4(n2−9)(2.66)
⇒9n2−36=10.66n2−96
∴1.66n2=60⇒n2=601.66=36
Similar Questions
A hydrogen like atom (atomic number z) is in a higher excited state of quantum number n. This excited atom can make a transition to the first excited state by successively emitting two photons of energies 10.2eV and 17.0eV respectively. Alternatively the atom from the same excited state can make a transition to the second excited state by successively emitting 2 photons of energy 4.25eV and5.95eV respectively. Determine the value of (n+z)
View Solutionएक हाइड्रोजन के समान परमाणु (परमाणु क्रमांक Z) किसी उच्च उत्तेजित अवस्था में है जिसकी क्वाण्टम संख्या (या कक्षा संख्या) n है | यह उत्तेजित परमाणु, प्रथम उत्तेजित अवस्था पर ऊर्जा क्रमश: 10.20 eV तथा 17.00 eV के दो फोटॉन उत्सर्जित करके आ सकता है तथा द्वितीय उत्तेजित अवस्था पर ऊर्जा क्रमश: 4.25 eV तथा 5.95 eV के दो फोटॉन उत्सर्जित करके आ सकता है | यदि हाइड्रोजन परमाणु की आयनन ऊर्जा 13.6 eV है तो n तथा Z के मान ज्ञात कीजिए |
View SolutionA hydrogen like, atom ( atomic number =Z) is in a higher excited state of quantum number n. This excited atom can make a transition to first excited state by successively emitting two photons of energies 10.20eV and 17.0 eV respectively. Alternatively, the atom from the same excited state can make a transition to second excited state by successively emitting two phons of energy 4.25 eV and 5.95eV respectively. Determine the values of n and Z.
View SolutionA hydrogen like species (atomic number Z) is present in a higher excited state of quantum number n. This excited atom can make a transitionn to the first excited state by successive emission of two photons of energies 10.20 eV and 17.0 eV respectively. Altetnatively, the atom from the same excited state can make a transition to the second excited state by successive of two photons of energy 4.25 eV and 5.95 eVv respectively. Determine the value of Z.
View SolutionA hydrogen atom (ionization potential 13.6 eV) makes a transition from third excited state to first excited state. The energy of the photon emitted in the process is _____eV.
View SolutionA hydrogen like atom of atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition to quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy(eV) that can be emitted by this atom during de - excitation. Ground state energy of hydrogen atom is -13.6 eV
View SolutionA hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited satte of quantum number n .This excited atom can make a transition to the first excited state by succesively emitting two photon of energies 10.20 eV and 17.00 eV .Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting twio photon of energy 4.25 ev and 5.95 eV Determine the followings: The atom during transition from n = 1 to n = 2 emit radiation in the region of
View Solution

