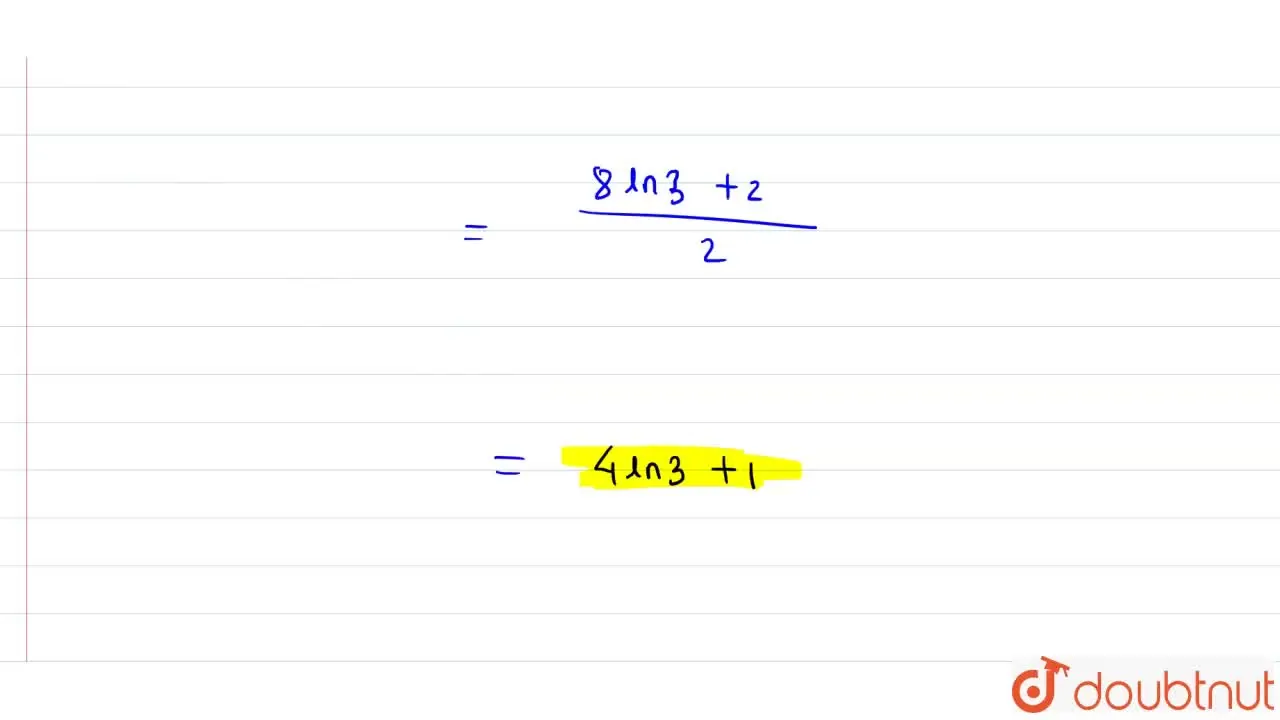Find the average value of μ of the function f(x) over the indicated intervals:
(a) f(x)=2x2+1 over [0, 1]
(b) f(x)=1x over [1, 2]
(c ) f(x)=3x−2x+3 over [0, 2]
Step by step video & image solution for Find the average value of mu of the function f(x) over the indicated intervals: (a) f(x) = 2x^(2) + 1 over [0, 1] (b) f(x) = (1)/(x) over [1, 2] (c ) f(x) = 3^(x)-2x + 3 over [0, 2] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas in Rectangular Coordinates25videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas with Parametrically Represented Boundaries7videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing the Limits of Sums with the Aid3videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS9videos
APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONS
- BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS5videos
BASIC CLASSES OF INTEGRABLE FUNCTIONS
Similar Questions
Find the average value μ of the function f(x)=3√x over the interval [0, 1]
View SolutionFind the average values of this functions:
(a) f(x)=sin2x over [0,2π] (b) f(x)=1ex+1 over [0, 2]View SolutionFind the greatest and the least values of the following functions on the indicated intervals :
f(x)=√(1−x)2(1+2x2) on[−1,1]View SolutionFind the value of c, of mean value theorem.when
(a) f(x)=√x2−4, in the interval [2,4]
(b) f(x)=2x2+3x+4 in the interval [1,2]
( c) f(x)=x(x−1) in the interval [1,2].View SolutionUsing Lagrange's theorem , find the value of c for the following functions :
(i) x3−3x2+2x in the interval [0,1/2].
(ii) f(x) = 2x2−10x+1 in the interval [2,7].
(iii) f(x) = (x-4) (x-6) in the interval [4,10].
(iv) f(x) = √x−1 in the interval [1,3].
(v) f(x) = 2x2+3x+4 in the interval [1,2].View SolutionThe value of b for which the function f(x)=x+cosx+b is strictly decreasing over R is:
a) b<1 b) b≤1 c) No value of b exists d) b≥1View SolutionThe value of b for which the function f(x)=x+cosx+b is strictly decreasing over R is:
a) b<1 b) b≤1 c) No value of b exists d) b≥1View SolutionVerify lagranges mean value theorem for the following functions on the indicated intervals. Also, find a point c in the indicated interval: f(x)=x(x−2)on[1,3] f(x)=x(x−1)(x−2)on[0,12].
View SolutionVerify the Lagrange's theorem for the following functions:
(a) f(x)=x3 in [−1,1]
(b) f(x)=sinx in [0,π2]
( c) f(x)=xn in [−1,1],n∈Z+
( d) f(x)=2x2−7x+10,x∈[2,5]View SolutiondIiscuss the global maxima/minima of following function in the given interval
f(x)=∣∣x2−4x+3∣∣∈[0.5].
(b) f(x)=3x4−2x3−6x2+6x+1∈[0,2].
(c) f(x)=√(1−x2)(1+2x2)∈[−1,1]
(d) f(x)=sinxsin2x∈(−∞,∞).View Solution