Question

Among the following , the plot that shows the correct marking of most probable velocity ${\displaystyle \left(V_{MP}\right)}$ average velocity ${\displaystyle \left(\overrightarrow{V}\right)}$ and root mean square velocity ${\displaystyle (V_{RMS}}$) is :

Options

A.
B.
C.
D.

Explanation

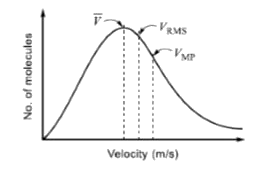
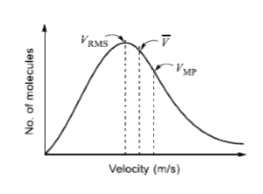
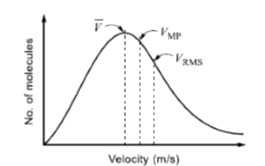
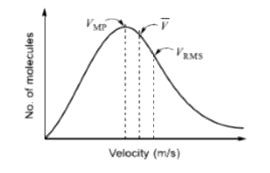
To solve the question about the correct marking of most probable velocity (V_MP), average velocity (V_avg), and root mean square velocity (V_RMS), we need to understand the relationships between these three types of velocities in the context of kinetic theory of gases.

1. Understand the Definitions:
- Most Probable Velocity (V_MP): This is the velocity of the molecules that is most likely to be found in a gas. It is given by the formula:
\( V_{MP} = \sqrt{\frac{2RT}{M}} \)
- Average Velocity (V_avg): This is the mean velocity of all the molecules in the gas. It is given by the formula:
\( V_{avg} = \sqrt{\frac{8RT}{\pi M}} \)
- Root Mean Square Velocity (V_RMS): This is the square root of the average of the squares of the velocities of the molecules. It is given by the formula:
\( V_{RMS} = \sqrt{\frac{3RT}{M}} \)

2. Calculate the Ratios:
- To compare the velocities, we can express them in terms of a common factor, which is \(\sqrt{\frac{RT}{M}}\):
- \(V_{MP} = \sqrt{2} \cdot \sqrt{\frac{RT}{M}} \approx 1.414 \cdot \sqrt{\frac{RT}{M}}\)
- \(V_{RMS} = \sqrt{3} \cdot \sqrt{\frac{RT}{M}} \approx 1.732 \cdot \sqrt{\frac{RT}{M}}\)
- \(V_{avg} = \sqrt{\frac{8}{\pi}} \cdot \sqrt{\frac{RT}{M}} \approx 1.596 \cdot \sqrt{\frac{RT}{M}}\)

3. Order the Velocities:
- From the calculated values:
- \(V_{MP} \approx 1.414\)
- \(V_{avg} \approx 1.596\)
- \(V_{RMS} \approx 1.732\)
- Therefore, the order from lowest to highest is:
\( V_{MP} < V_{avg} < V_{RMS} \)

4. Identify the Correct Plot:
- Based on the order of velocities, we need to find the plot that correctly marks:
- V_MP (lowest)
- V_avg (middle)
- V_RMS (highest)
- According to the analysis, the correct option is D, where V_RMS is the highest, followed by V_avg, and V_MP is the lowest.

Conclusion:
The correct answer is Option D.