Consider a regular 10-gon with its vertices on the unit circle. With one vertex fixed, draw straight lines to the other 9 vertices. Call them $L_{1}, L_{2}, \dots . L_{9}$ and denote their lengths by $l_{1}, l_{2} \dots . l_{9}$ respectively. Then the product $l_{1} l_{2} ... . l_{9}$ is

$10 \sqrt{3}$

$\frac{50}{\sqrt{3}}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to find the product of the lengths of the lines drawn from a fixed vertex of a regular 10-gon inscribed in a unit circle to the other 9 vertices. We denote the lengths of these lines as $l_{1}, l_{2}, \dots, l_{9}$ .
1. Understanding the Regular 10-gon:
A regular 10-gon has 10 vertices that are evenly spaced on the unit circle. The vertices can be represented using complex numbers as the 10th roots of unity.
2. Vertices Representation:
The vertices of the 10-gon can be expressed as:
$z_{k} = e^{2 π i k / 10} for k = 0, 1, 2, \dots, 9$
where $z_{0} = 1$ is the fixed vertex.
3. Calculating Lengths:
The lengths $l_{k}$ from the fixed vertex $z_{0}$ to the other vertices $z_{k}$ (for $k = 1, 2, \dots, 9$ ) are given by:
$l_{k} = | z_{0} - z_{k} | = | 1 - e^{2 π i k / 10} |$
4. Using the Formula for Lengths:
We can simplify $l_{k}$ :
$l_{k} = | 1 - (cos (2 π k / 10) + i sin (2 π k / 10) | = \sqrt{(1 - cos (2 π k / 10))^{2} + {sin}^{2} (2 π k / 10)}$
Using the identity ${sin}^{2} x + {cos}^{2} x = 1$ , we can simplify further:
$l_{k} = \sqrt{2 - 2 cos (2 π k / 10)} = 2 sin (\frac{π k}{10})$
5. Product of Lengths:
Now we need to calculate the product:
$P = l_{1} l_{2} \dots l_{9} = 9 \prod k = 1 2 sin (\frac{π k}{10}) = 2^{9} 9 \prod k = 1 sin (\frac{π k}{10})$
6. Using the Product Identity:
We can use the identity for the product of sines:
$n - 1 \prod k = 1 sin (\frac{k π}{n}) = \frac{n}{2^{n - 1}}$
For $n = 10$ :
$9 \prod k = 1 sin (\frac{π k}{10}) = \frac{10}{2^{9}}$
7. Final Calculation:
Substituting back into our product:
$P = 2^{9} \cdot \frac{10}{2^{9}} = 10$
Conclusion:
The product $l_{1} l_{2} \dots l_{9}$ is equal to $10$ .

Updated on:7/8/2024

In Fig., there are two convex lenses $L_{1}$ and $L_{2}$ having focal lengths $F_{1}$ and $F_{2}$ respectively. The distance between $L_{1}$ and $L_{2}$ will be :

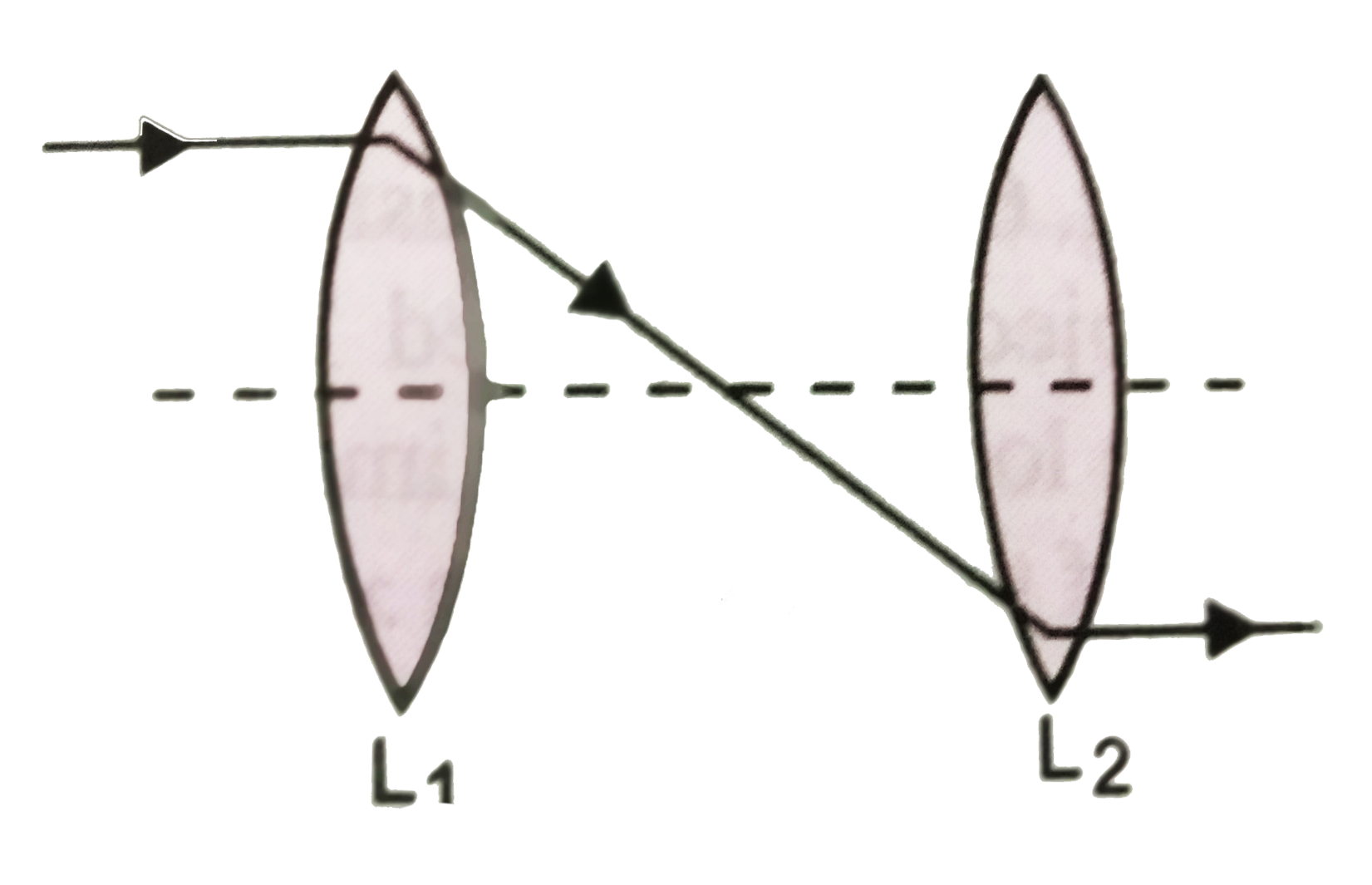A $F_{1}$
B $F_{2}$
C $F_{1} + F_{2}$
D $F_{1} - F_{2}$
In the figure shown, there are two convex lenses $L_{1}$ and $L_{2}$ having focal. Lengths $f_{1}$ and $f_{2}$ respectively. The distance between $L_{1}$ and $L_{2}$ will be

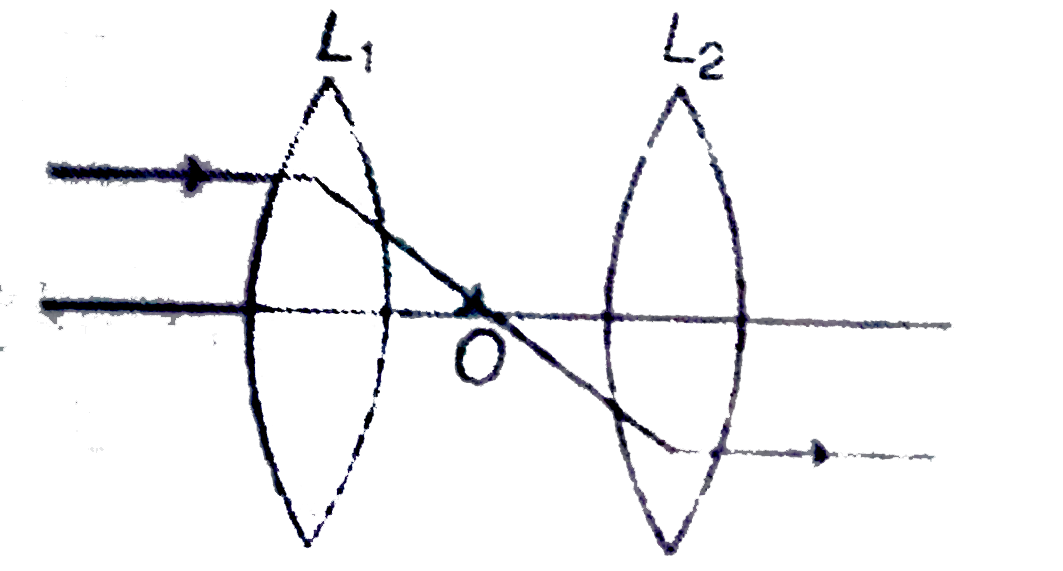A $f_{1}$
B $f_{2}$
C $f_{1} + f_{2}$
D $f_{1} - f_{2}$
Two wires of equal diameters, of resistivities $ρ_{1}$ and $ρ_{2}$ and length $l_{1}$ and $l_{2}$ , respectively of the combination is
A $\frac{ρ_{1} l_{1} + ρ_{2} l_{2}}{l_{1} + l_{2}}$
B $\frac{ρ_{1} l_{2} + ρ_{2} l_{1}}{l_{1} - l_{2}}$
C $\frac{ρ_{1} l_{2} + ρ_{2} l_{1}}{l_{1} + l_{2}}$
D $\frac{ρ_{1} l_{1} + ρ_{2} l_{2}}{l_{1} - l_{2}}$