A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
![A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R = 1 M Omega across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t = 10^(-3) s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t// tau)], where the time constant tau is equal to CR.)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_TEL_PHY_XII_P1_C08_SLV_001_Q01.png) Solution in Telugu
Solution in Telugu
The time constant of the CR circuit is τ=CR=10−3 s. Then, we have
q(t)=CV[l−exp(−t/τ)]
=2×10−9[1−exp(−t/10−3]
The electric field in between the plates at time t is A=π(l)2m2 = area of the plates. Consider now a circular loop of radius [ 1/2) m parallel to the plates passing through P. The magnetic field B at all points on the loop is along the loop and of the same value. Then flux
E×π×122=πE4=q4ε0
The displacement current
Now applying amere maxwell law to the loop we get
or B=0.74×10−13 T
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -IA
54 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -IB
39 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise
10 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
Similar Questions
The idea of displacement current was introduced by
View Solution(A ): Induced electric fields are produced by time varying magnetic field. (R): According to faraday’s law ∮→E.→dl=dϕdt
View SolutionConsider Experiment II in Section 6.2.
a. What would you do to obtain a large deflection of the galvanometer?
b. How would you demonstrate the presence of an induced current in the absence of a galvanometer?
View SolutionWhat is the radius of the path of an electron (mass 9 × 10-31 kg and charge 1.6×x10–19 C) moving at a speed of 3×x107 m/s in a magnetic field of 6x×10−4 T perpendicular to it? What is its frequency? Calculate its energy in keV. (1eV=1.6×10−19J)
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 0.5muF. At t=0, it is connected for charging inseries with a resistance R=2kOmega across a 4V battery. Calculate the magnetic field at a point P in between the plates and half way between the centre and periphery of the plates after 10^-3s . Fig.
View SolutionA parallel plate capacitor has an electric field of 10^(5)V//m between the plates. If the charge on the capacitor plate is 1muC , then force on each capacitor plate is-
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF . At t = 0 , it is connected for charging in series with a resistor R = 1MOmega across a 2V battery. Calculate the magnetic field at a point P , halfway between the cnetre and the periphery of the plates, after t = 10^(-3)sec .
View SolutionA parallel plate capacitor with circular plates of radius 1m has a c apacitance of 1n F. At t=0,it is connected for charging in series with a resistance R=1MΩ across2V battery . Calculate the magnetic field at a point P, in between the plates and half way between the centre and the periphery of the plates after 10−3s.
View Solutionएक समांतर प्लेट संधारित्र जिसकी व्रत्ताकार प्लेटों की त्रिज्या 1m है धारिता 1nf है। समय t = 0 पर इसको आवेशित करने के लिए R= 1 MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोडा गया है (चित्र 8.3) । 10−3s ds पश्चात संधारित्र के बीच में दोनों प्लेटों के केंद्र एवं उनकी परिमिति के ठीक मध्य में स्थित बिंदु P पर चुंबकीय क्षेत्र का परिकलन कीजिए । [क्षण t पर संधारित्र पर आवेश q(t)=CV[1–exp(−t/π)] होता है जहाँ समय नियतांक τ=CR है ]।

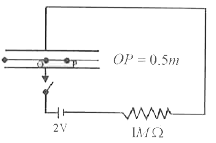
View Solutionकिसी समांतर प्लेट संधारित्र की वृत्ताकार प्लेटो की त्रिज्या 1 m तथा धारिता C=1nF है। इसे चित्र 1।9 के अनुसार 2 V की बैटरी तथा 1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में जोड़ा गया है। आवेशित करने के लिए सलंगन स्विच को समय t = 0 पर बंद किया जाता है समय t=1ms पर संधारित्र के बीच में दोनों प्लेटो के केंद एव उसकी परिमिति के ठीक माध्य में स्थति बिंदु P पर चुंबकीय क्षेत्र का मान ज्ञात करे। मान ले कि आवेशन के क्रम संधारित्र पर आवेश का तात्कालिक मान है- q(t)CV(1−etCR)
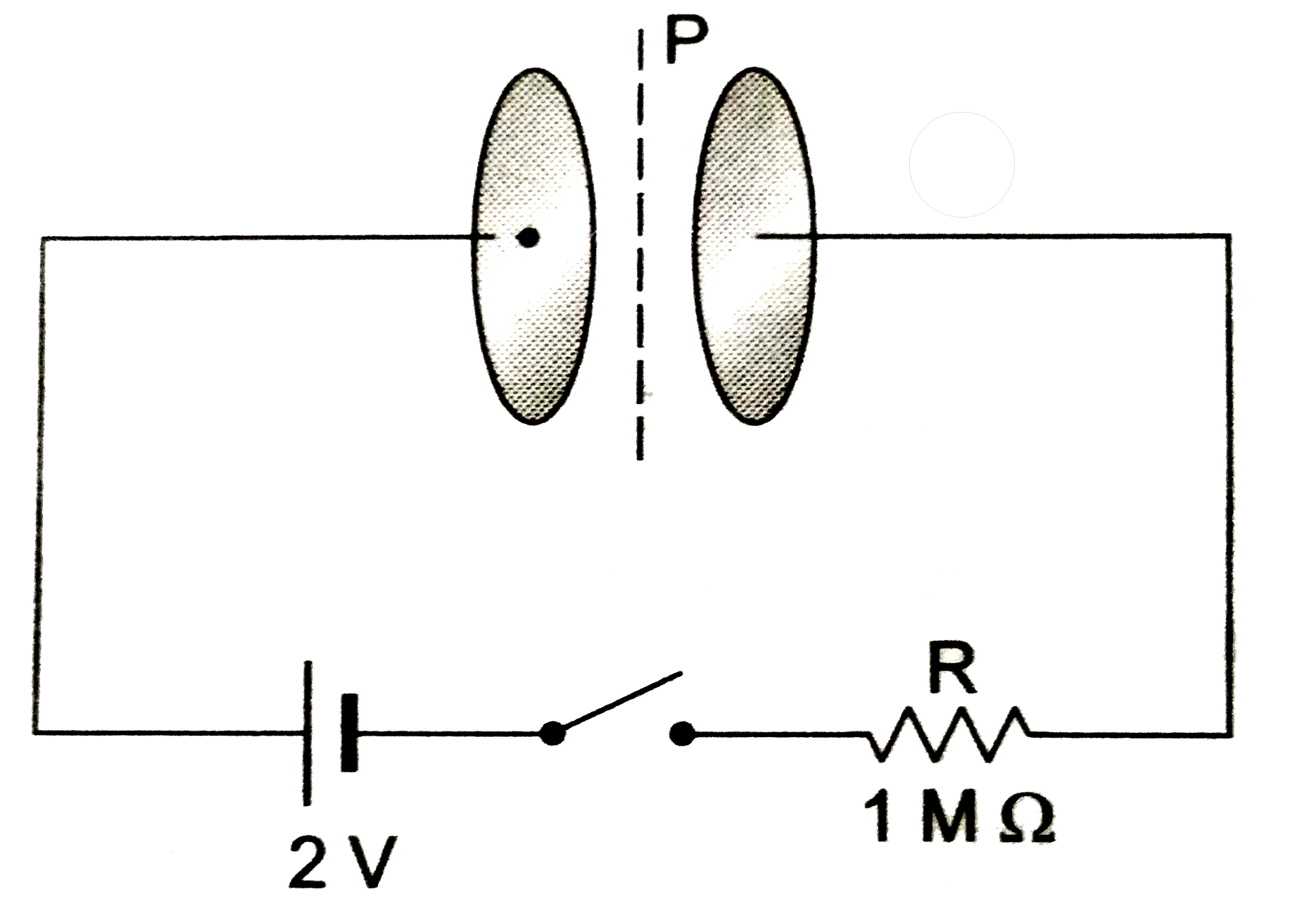
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1 nF. At t=0 , It is connected for charging in series with are resistor R=1 M Q across a 2V battery (fig). Calculate the magnetic field at a point P halfway between the centre and the periphery of the plates. after t=10−3s. (The charge on the capacitor at time τ is q(t) CV [1 =exp (−t/τ) ], where the time constant τ is equal to CR).
View SolutionA parallel plate capacitor has an electric field of 10^(5)V//m between the plates. If the charge on the capacitor plate is 1muC , the force on each capacitor plate is
View Solutionएक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m है धारिता 1nF है समय t =0 पर इसको आवेशित करने के लिए R=1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोड़ा गया है ( चित्र ) 10−3S के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं परिकलन कीजिए [क्षण t पर संधारित्र पर आवेश q(t)=CV[1−exp(−t/t) होता है जहाँ समय नियतांक τ=CR है
View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1nF. At t = 0, it is connected for chargeing in series with a resistor R=1 M Omega across a 2V battery (Figure). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s . (The charge on the capacitor at time t is q(t)=CV[1-exp((-t)/(tau))] , where the time constant tau is equal to CR).
View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)

View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
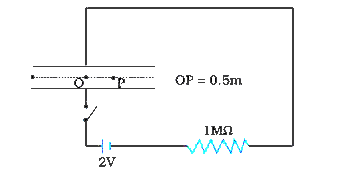
View Solution
