The potential energy U between two molecules as a function of the distance X between them has been shown in the Fig. The two molecules are
 Solution in Telugu
Solution in Telugu
Attracted when X lies between A and B and are repelled when X lies between B&C
Attracted when X lies between B and C and are repelled when lies between A & B
Attracted when they reach B.
Repelled when they reach B
The correct Answer is:B
Step by step video, text & image solution for The potential energy U between two molecules as a function of the distance X between them has been shown in the Fig. The two molecules are by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE -IA (MATCHING)
4 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE -IA (ASCENDING OR DESCENDING ORDER)
4 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-3
43 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise
84 Videos
Similar Questions
A spring of young's modulus 2×1011 pa is suspended vertically and subjected to a load of 5 kg and elongation is 2 mm. when the load is doubled - match the following (g=9.8m/s2)
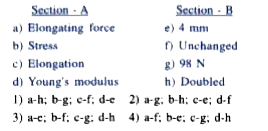
View SolutionFour springs of force constants K1=1000N/m,K2=1500N/m,K3=2500N/mand K4=2000N/m are subjected to different loads producing same extension. Arrange the springs with work done in descending order
View SolutionA wire of length 1m and radius 1mm is subjected to a load. The extension is 'x'. The wire is melted and then drawn into a wire of square cross-section of side 1mm. What is its extension under the same load?
View SolutionA U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5cm of spirit in the other. What is the specific gravity of spirit.
View SolutionA person runs along a circular path of radius 5m. Find the magnitude of the displacement if he runs all the way around the circle ?
View Solution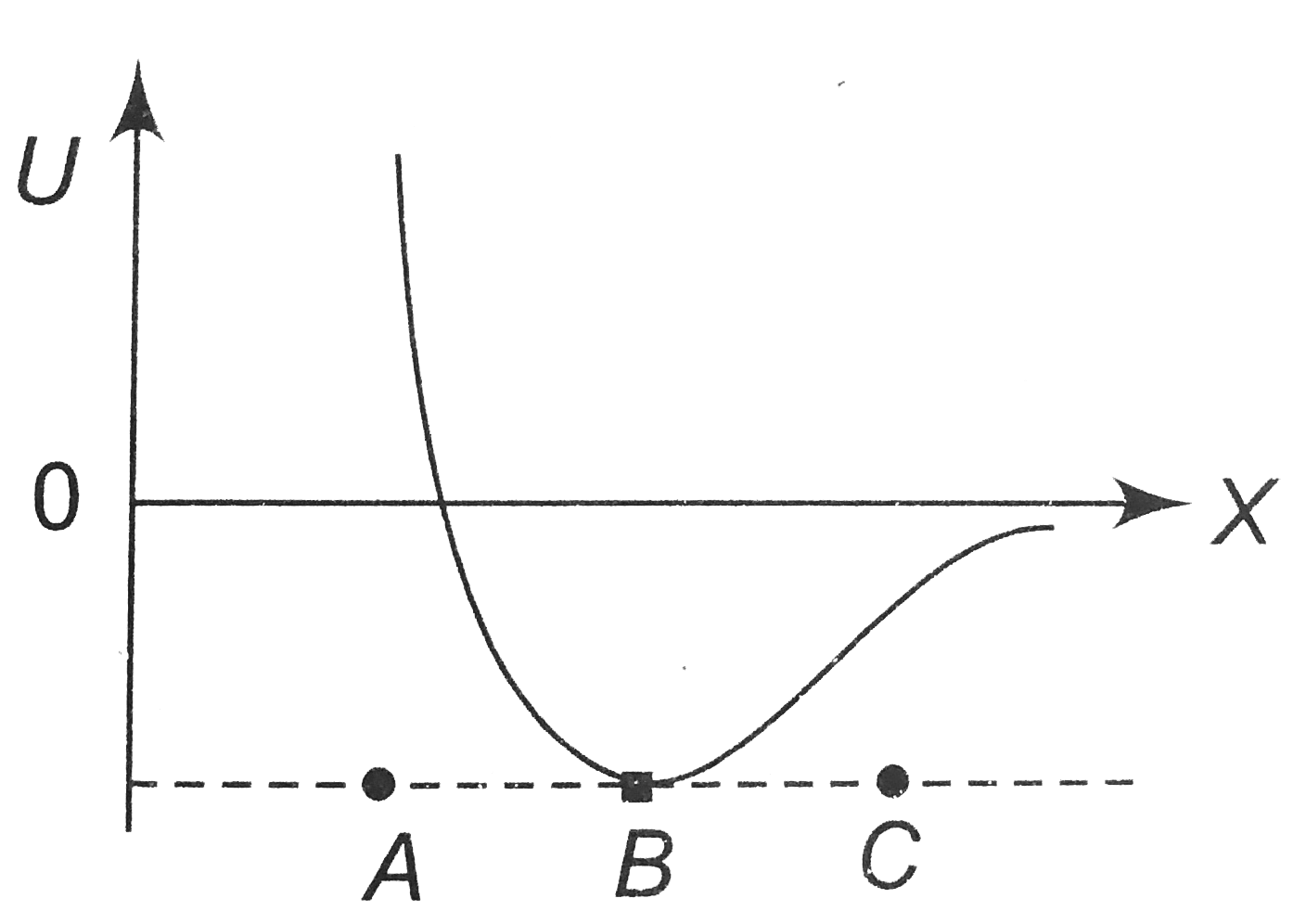
The potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are
View SolutionThe potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two moleucles are
View SolutionThe potential energy U between two molecules as a function of the distance X between them has been shown in the figure. The two molecules are

View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x)=ax12−bx6 where a and b are constant and x is the distance between the atoms. Find the dissoociation energy of the molecule which is given as D=[U(x−∞)−Uatequilibrium]
View SolutionIf the potential energy between two molecules is given by U= -(A)/(r^6) + B/(r^(12)) , then at equilibrium , separation between molecules , and the potential energy are :
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x)=a/(x^(12))-b/(x^(6)) , where a and b are constants ans x is the distance between the atoms. If the dissociation energy of the molecule is D = [U(x = oo) - U_(at) equilibrium ] , D is :
View Solutionएक द्विपरमानुक अणु में दो परमाणुओं के बीच लग रहे बल के लिए स्थितिज ऊर्जा फलन लगभग U(x)=ax12−bx6 से दिया जाता है जहाँ a एवं b स्थिरांक है और x परमाणुओं के बीच दूरी है। यदि अणु की विघटन ऊर्जा D=[U(x=∞)−U साम्यावस्था पर] है , तब D है
View SolutionThe potential energy (U) between two atoms in a diatomic molecule as a function of the distance x between atoms has been shown in the adjoining figure. The atoms are
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x)=ax12−bx6 where a and b are constant and x is the distance between the atoms. Find the dissoociation energy of the molecule which is given as D=[U(x−∞)−Uatequilibrium]
View SolutionIf the potential energy between two molecules is given by U= -(A)/(r^6) + B/(r^(12)) , then at equilibrium , separation between molecules , and the potential energy are :
View Solution
