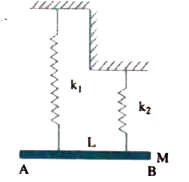
When a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
 Solution in Telugu
Solution in Telugu
As it given that the mass M stretches the original spring by a distance x,
we have kx=Mg (or) k=Mgx......... (1)
The new force constants of the two springs can be given by using equations
k1=kegll1andk2=keqll2as,k1=3kandk2=3k2
Let we take the stretch in the two springs be x1andx2 we have for the equilibrium of the rod
k1x1+k2x2=Mg (or) 2kx1+3k2x2=Mg
From equation (1) , we have x1+x22=x3......... (2)
As the rod is horizontal and in static equilibrium , we have net torque acting on the rod about any point on it must be zero. Thus we have torquie on it above end A are
k2x2L=Mg(L)2
(or) x2=Mg2k2=Mg3k=x3
Using this value of x2 in equation (2) ,
we have x1=x6
This can also be directly obtained by using torque zero about point B on the rod as
k1x1L=Mg(L)2
(or) x1=Mg2k1=Mg6k=x6
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:LONG ANSWER TYPE QUESTIONS
Explore 2 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:SHORT ANSWER TYPE QUESTION
Explore 2 Videos
- KINETIC THEORY OF GASESBook:AAKASH SERIESChapter:KINETIC THEORY OF GASESExercise:Practice Exercise
Explore 15 Videos
- MECHANICAL PROPERTIES OF FLUIDS Book:AAKASH SERIESChapter:MECHANICAL PROPERTIES OF FLUIDS Exercise:EXERCISE-3
Explore 43 Videos
Similar Questions
Two unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
View SolutionTwo blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M, what is the contact force between the two blocks?
View SolutionThe kinetic energy of translation of 20gm of oxygen at 47∘C is (molecular wt. of oxygen is 32gm/mol and R=8.3 J/mol/K)
View SolutionA U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5cm of spirit in the other. What is the specific gravity of spirit.
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
View SolutionA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
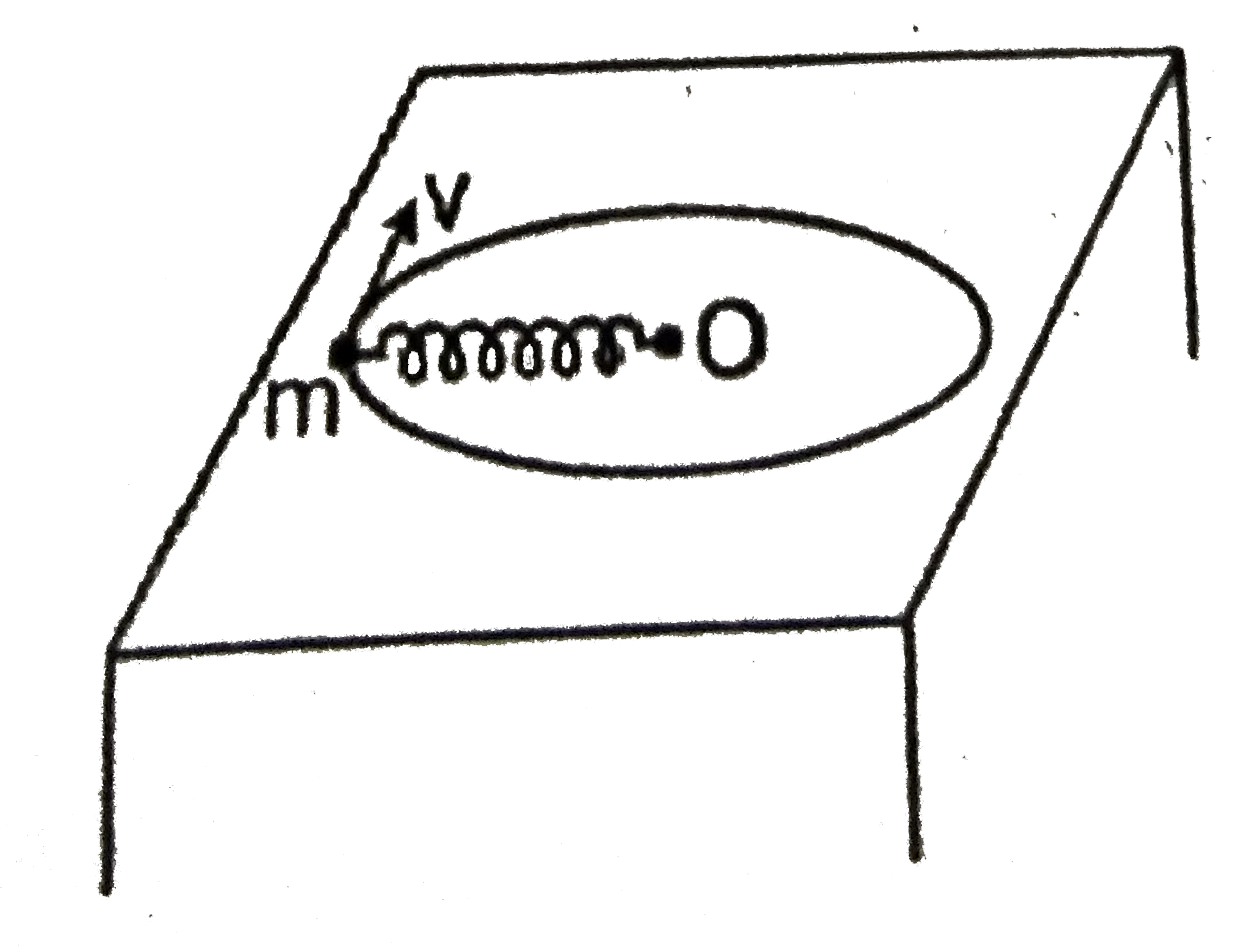
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
View SolutionA horizontal metallic rod of mass m and length l is supported by two vertical identical springs of spring constant k each and natral length i_(0) A current l is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of lengths l//3 and 2l//3 , and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure-2.111. Find the stretch in each of the spring.
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
View Solutionस्प्रिंग नियतांक K की एक स्प्रिंग पर m द्रव्यमान लटकाया गया है। अब स्प्रिंग को दो बराबर भागों में काटकर किसी एक पर ही द्रव्यमान लटकाया जाता है , तो नया स्प्रिंग नियतांक होगा
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l//3"and" 2l//3 , and two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure . Find the stretch in each of the spring
View Solution
