A stationary body explodes into four identical fragments such that three of them fly off mutually perpendicular to each other, each with same K.E. E0. The energy released in the explosion in the form of kinetic energy is NE0. Find N Solution in Telugu
The correct Answer is:6
Step by step video, text & image solution for A stationary body explodes into four identical fragments such that three of them fly off mutually perpendicular to each other, each with same K.E. E_(0). The energy released in the explosion in the form of kinetic energy is NE_(0). Find N by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
36 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MATRIX MATCHING TYPE QUESTIONS)
1 Video
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
The velocity of a particle of mass 10−2kg is given as →v=(2xˆu+3yˆj+4zˆk) m/sec (where x, y and z are in meter). The amount of work done by applied force in displacing a particle from (1m, 2m, 0) to (-1m, 3m, 1m) is …..
View SolutionAn automobile of mass m accelerates, starting from rest while engine supplied constant power p. Match the following columns (after t sec).
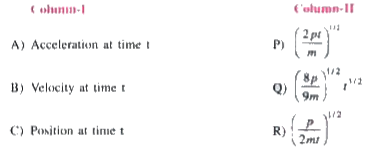
View SolutionAn iron sphere of mass 20×10−3 kg falls through a viscous liquid with terminal velocity 0.5 m/sec. Find the terminal velocity of another iron sphere of mass 54×10−2 kg.
View SolutionIf →A+→B=→Rand2→A+→B is perpendicular to →B then
View SolutionA particle of mass 4 m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The total energy released in the process of explosion is ............
View SolutionA stationary body explodes into two fragments of masses m_(1) and m_(2) . If momentum of one fragment is p , the energy of explosion is
View SolutionA stationary body explodes in to four identical fragments such that three of them fly mutually perpendicular to each other, each with same KE(E0). The energy of explosion will be
View SolutionA stationary body explodes into two fragments of masses m1 and m2. If momentum of one fragment is p, the energy of explosion is
View SolutionA spaceship while flyting in space, splits up into three equal parts, due to an explosion. One fragment keeps moving in the same direction, the other two fly of at 60∘ to the original direction , on either side. If the energy released due to the explosion is twice the kinetic energy of the spaceship, find the kinetic energy of each of the fragment.
View SolutionA body kept at rest explodes in four identical fragments and it is found that three of them move along mutually perpendicular directions with same kinetic energy K . Total energy released in the explosion is
View SolutionA stationary shell explodes into two fragments, having masses in the ratio of 1:2. The heavier fragment attains a Kinetic energy of 100J. The Kinetic energy released in the explosion is:
View SolutionA stationary shell explodes into two fragments, having masses in the ratio of 1:2. The heavier fragment attains a Kinetic energy of 100J. The Kinetic energy released in the explosion is
View SolutionA body of mass 4m at rest explodes into three fragments. Two of the fragments each of mass m move with speed v in mutually perpendicular directions. Total energy released in the process is
View SolutionA stationary body explodes into two fragments of masses m_(1) and m_(2) . If momentum of one fragment is p , the energy of explosion is
View SolutionA stationary body explodes in to four identical fragments such that three of them fly mutually perpendicular to each other, each with same KE(E0). The energy of explosion will be
View Solution
