कथन-1 : बिन्दु (2a,0) से होकर जाने वाले वृत्त का समीकरण x2+y2−2ax=0 होगा। जिसका मूलाक्ष वृत्त x2+y2=a2 के सापेक्ष x=a2 है,
कथन-2 : दो वृत्तों x2+y2+2g1x+2f1y+c1 तथा x2+y2+2g2x+2f2y+c2=0 के मूलाक्षों का समीकरण 2(g1−g2)x+2(f1−f2)y+(c1−c2)=0 है।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है।
कथन -1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
The correct Answer is:A
Step by step video, text & image solution for कथन-1 : बिन्दु (2a,0) से होकर जाने वाले वृत्त का समीकरण x^(2)+y^(2)-2ax=0 होगा। जिसका मूलाक्ष वृत्त x^(2) +y^(2) = a^(2) के सापेक्ष x=(a)/(2) है, कथन-2 : दो वृत्तों x^(2)+y^(2)+2g_(1)x+2f_(1)y+c_(1) तथा x^(2)+y^(2)+2g_(2)x+2f_(2)y+c_(2)=0 के मूलाक्षों का समीकरण 2(g_(1)-g_(2))x+2(f_(1)-f_(2))y+(c_(1)-c_(2))=0 है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Comprehension type questions)46videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Matrix Match type questions)8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (More than one correct answers)28videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)7videos
शांकव परिच्छेद
Similar Questions
समबाहु त्रिभुज PQR के अंतनिर्हित एक वृत C स्थित है जिसकी त्रिज्या 1 है। त्रिभुज की भुजाओ PQ, QR, RF को बिंदु D, E, F पर स्पर्श करता है। रेखा PQ का समीकरण √3x+y−6=0 तथा बिंदु D(3√32,32) है। यह भी दिया है की मूलबिंदु व C का केंद्र रेखा PQ के एक तरफ ही स्थित है।
वृत C का समीकरण है05:45View Solutionकॉलम I में दिए गए वक्त्तव्यों का कॉलम II में दिए गए गुणधर्मों से सुमेल करें
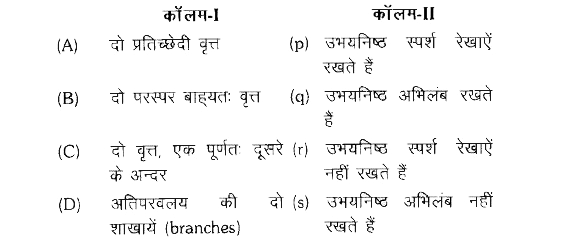
04:01View Solutionमाना कि L1 मूलबिन्दु से गुजरने वाली एक सरल रेखा है तथा सरल रेखा L2 का समीकरण x+y=1 है। यदि वृत्त x2+y2−x+3y=0 द्वारा L1 और L2 पर काटे गये अन्तःखण्ड बराबर हैं, तो निम्नलिखित में से कौन-सा समीकरण रेखा L1 को निरूपित करता है
01:56View Solution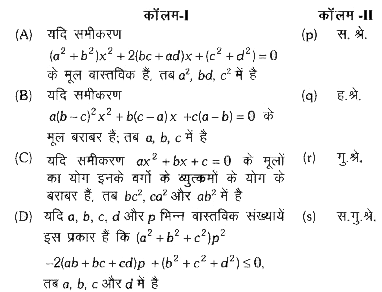
View Solution
08:42View SolutionIf the two circles,x^(2)+y^(2)+2g_(1)x+2f_(1)y=0delta x^(2)+y^(2)+2g_(2)x+2f_(2)y=0 touch each other then (1)f_(1)g_(1)=f_(2)g_(2)(2)(f_(1))/(g_(1))=(f_(2))/(g_(2))(3)f_(1)f_(2)=g_(1)g_(2)(4) none of these
05:01View SolutionThe solution of ((dy)/(dx))^(2)+(2x+y)(dy)/(dx)+2xy=0, is (i) (y+x^(2)-c_(1))(x+log y+y^(2)+c_(2))( (ii) (y+x^(2)-c_(1))(x-log y-c_(2))( iii) (y+x^(2)-c_(1))(x+log y-c_(2))( iv) (y+x^(2)-c_(1))(3x+log y-c_(2))
02:45View SolutionThe circles ax2+ay2+2g1x+2f1y+c1=0 and bx2+by2+2g2x+2f2y+c2=0
(a≠0andb≠0) cut orthogonally, if08:22View Solutionयदि वृत्त x2+y2+2g1x+2f1y=0 तथा x2+y2+2g2x+2f2y=0 एक-दूसरे को स्पर्श करें तो सिद्ध कीजिए की f1g2=f2g1
02:40View Solutionदो वक्र c1=y2=4x व c2=x2+y2−6x+1=0 हैं, तब-
08:03View SolutionIf circles x2+y2+2g1x+2f1y=0 and
x2+y2+2g2x+2f2y=0 touch each other, then03:51View SolutionThe line a1x+b1y+c1=0 and a2x+b2y+c2=0 are perpendicular if:
05:10View Solutionदो वृत्त S1=x2+y2+2g1x+2f1y+c1=0 तथा S2=x2+y2+2g2x+2f2y+c2=0 परस्पर लम्ब कोणी है यदि
06:51View SolutionThe circles ax2+ay2+2g1x+2f1y+c1=0 and bx2+by2+2g2x+2f2y+c2=0 (a≠0 and b≠0) cut orthogonally if
04:40View SolutionNews x^(2) + y^(2) + 2 g_(1) x - a^(2) = "0 व" x^(2) + y^(@) + 2g_(2) x - a^(2) = 0 Are mutually perpendicular. If the length of the length of the tangent of these circles from (0, a) and (0, -a) p_(1), p_(2) Are then p_(1), p_(2) The value of
08:05View SolutionStatement - 1: Equation of circle passing through point (2a, 0) x^(2)+y^(2)-2ax=0 Will happen. Whose radix circle x^(2) +y^(2) = a^(2) relative to x=(a)/(2) is, Statement 2: Two circles x^(2)+y^(2)+2g_(1)x+2f_(1)y+c_(1) And x^(2)+y^(2)+2g_(2)x+2f_(2)y+c_(2)=0 The equation of radixes 2(g_(1)-g_(2))x+2(f_(1)-f_(2))y+(c_(1)-c_(2))=0 is.
04:06View Solution