यदि एक अचर त्रिज्या 3k का वृत्त मूल बिन्दु से गुजरता है एवं अक्षों को A व B पर मिलता है, तो त्रिभुज OAB के केन्द्रक का बिन्दुपथ है
x2+y2=k2
x2+y2+k2=0
x2+y2+4k2=0
x2+y2=4k2
The correct Answer is:D
Step by step video, text & image solution for यदि एक अचर त्रिज्या 3k का वृत्त मूल बिन्दु से गुजरता है एवं अक्षों को A व B पर मिलता है, तो त्रिभुज OAB के केन्द्रक का बिन्दुपथ है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (More than one correct answers)28videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Reasoning type questions )8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - Solved Multiple Choice Questions (वृत्त की स्पर्श रेखा तथा अभिलम्ब)72videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)7videos
शांकव परिच्छेद
Similar Questions
माना कि L1 मूलबिन्दु से गुजरने वाली एक सरल रेखा है तथा सरल रेखा L2 का समीकरण x+y=1 है। यदि वृत्त x2+y2−x+3y=0 द्वारा L1 और L2 पर काटे गये अन्तःखण्ड बराबर हैं, तो निम्नलिखित में से कौन-सा समीकरण रेखा L1 को निरूपित करता है
02:37View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।05:04View Solutionरेखा lx+my+n=0 वृत्त x2+y2=a2 की एक स्पर्श रेखा होगी यदि
02:39View Solution
03:50View Solution
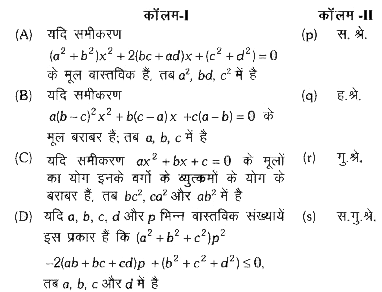
03:15View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
03:18View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
04:39View Solutionनिम्नलिखित स्थितियों में एक चर बिंदु का बिन्दुपथ ज्ञात कीजिए जिसकी
दोनों अक्षों से दूरियों का योग एक अचर राशिc है ।06:02View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
03:38View Solutionयदि O मूल बिन्दु तथा A(a,b,c) है तो A से जाने वाले एवं OA लम्ब समतल का समीकरण है -
04:32View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
03:59View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
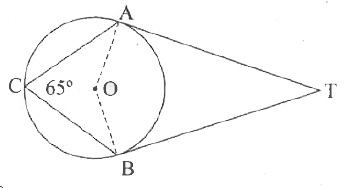
02:32View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -
06:20View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
04:26View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
05:40View Solutionएक बिंदु P,2x−3y+4=0 पर गति करता है । यदि Q(1,4) तथा R(3,-2) निश्चित बिंदु है, तो ΔPQR के केन्द्रक का बिन्दुपथ (locus) एक रेखा है
06:39View Solution