The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-
![The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T(2) and T(1)(T(2)gtT(1)). The rate of heat of heat transfer through the slab, in ? steady state is [(A(T(2)-T(1))/(x)]f, with f equal to :-](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E09_013_Q01.png)
Step by step video & image solution for The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T_(2) and T_(1)(T_(2)gtT_(1)). The rate of heat of heat transfer through the slab, in ? steady state is [(A(T_(2)-T_(1))/(x)]f, with f equal to :- by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Thermal Properties of MatterBook:SL ARORAChapter:Thermal Properties of MatterExercise:Exercise
Explore 449 Videos
- System of particles & rotational MotionBook:SL ARORAChapter:System of particles & rotational MotionExercise:EXERCISE
Explore 353 Videos
- THERMODYNAMICSBook:SL ARORAChapter:THERMODYNAMICSExercise:Exercise
Explore 342 Videos
Similar Questions
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
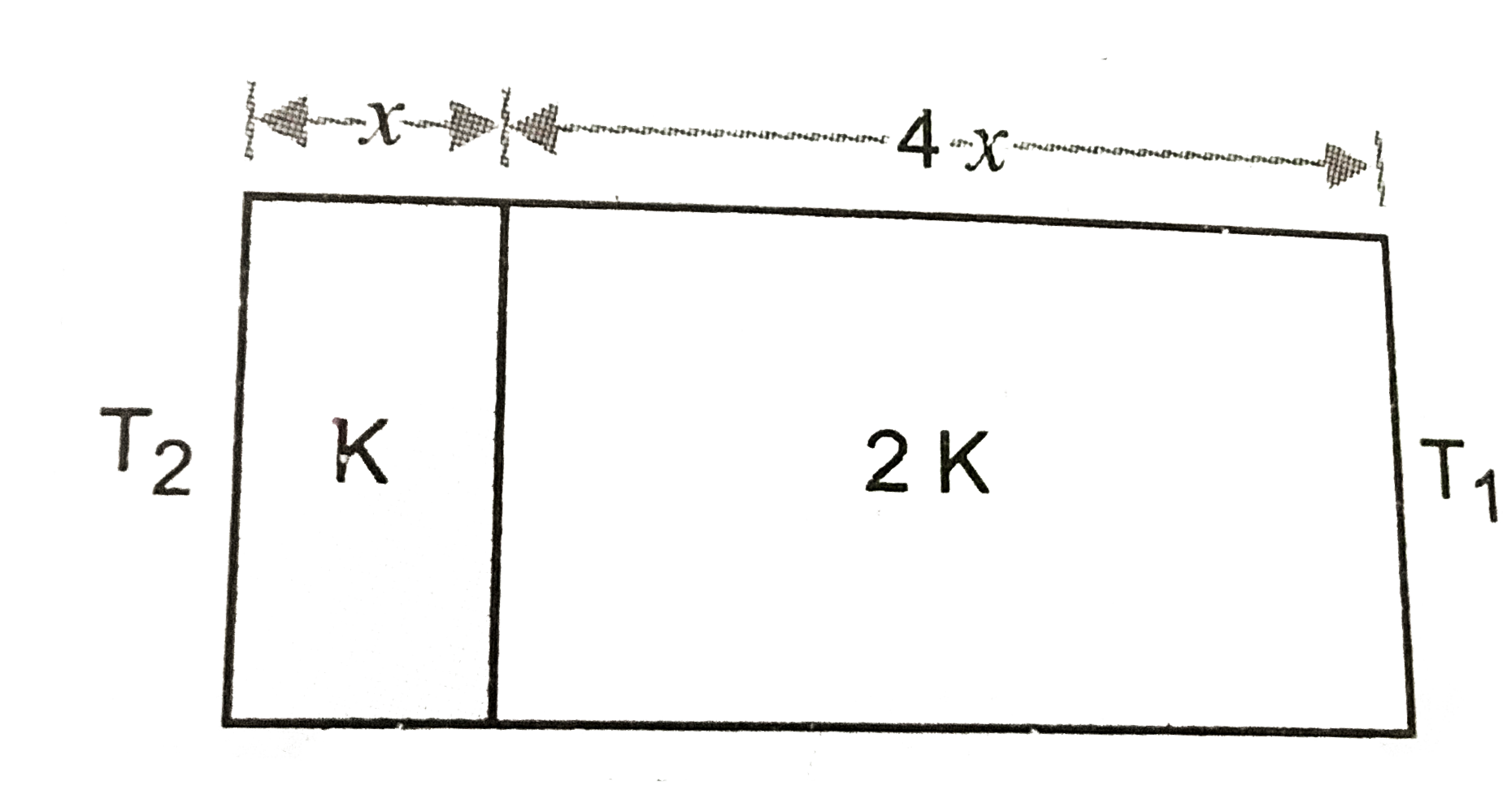
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
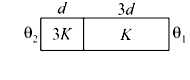
View Solution
Knowledge Check
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .A1B1/2C2/3D1/3
.A1B1/2C2/3D1/3
Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

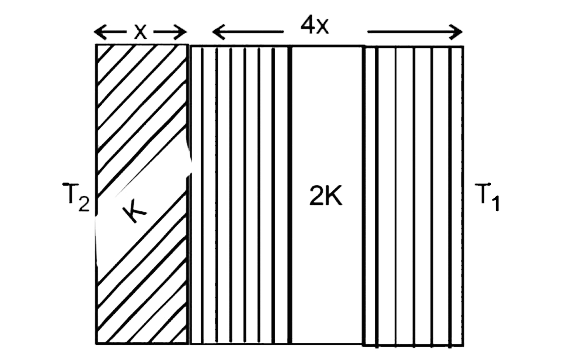
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materails having coefficients of two materails having coefficients of termal conductivity K and 2K and thickness x and 4x, respectively, are T2andT1(T1>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)K2)f, with f equal to
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View Solution

