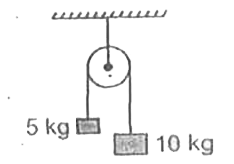Two masses as shown are suspended from a massless pulley. Calculate the acceleration of the system when masses aere left free:
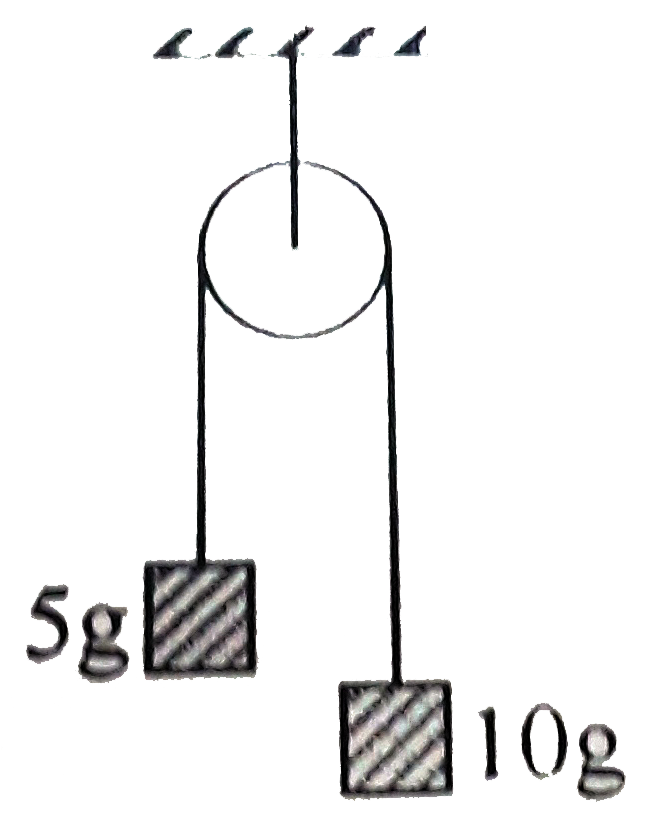
2g3
g3
g9
g7
Step by step video & image solution for Two masses as shown are suspended from a massless pulley. Calculate the acceleration of the system when masses aere left free: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
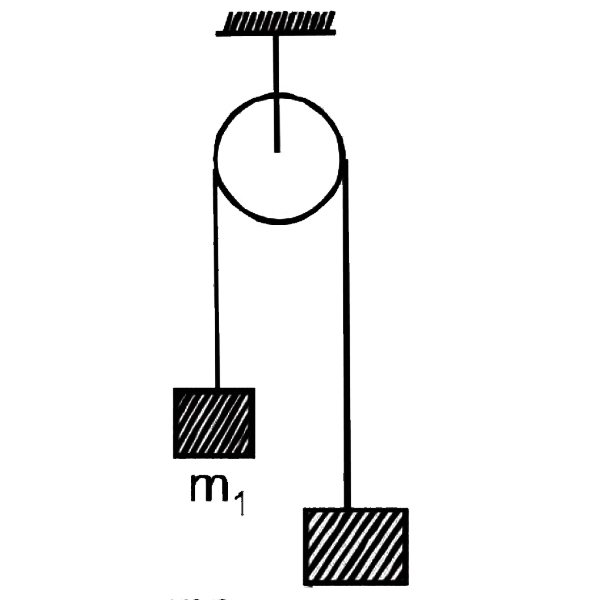
Two masses m1=5kg and m2=4.8kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move?
 A(a) 5m/s2B(b) 9.8m/s2C(c) 0.2m/s2D(d) 4.8m/s2
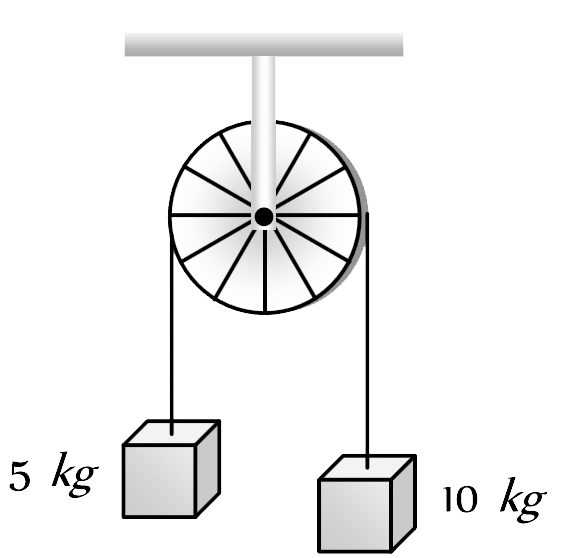
A(a) 5m/s2B(b) 9.8m/s2C(c) 0.2m/s2D(d) 4.8m/s2USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
 AgBg2Cg3Dg4
AgBg2Cg3Dg4In the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
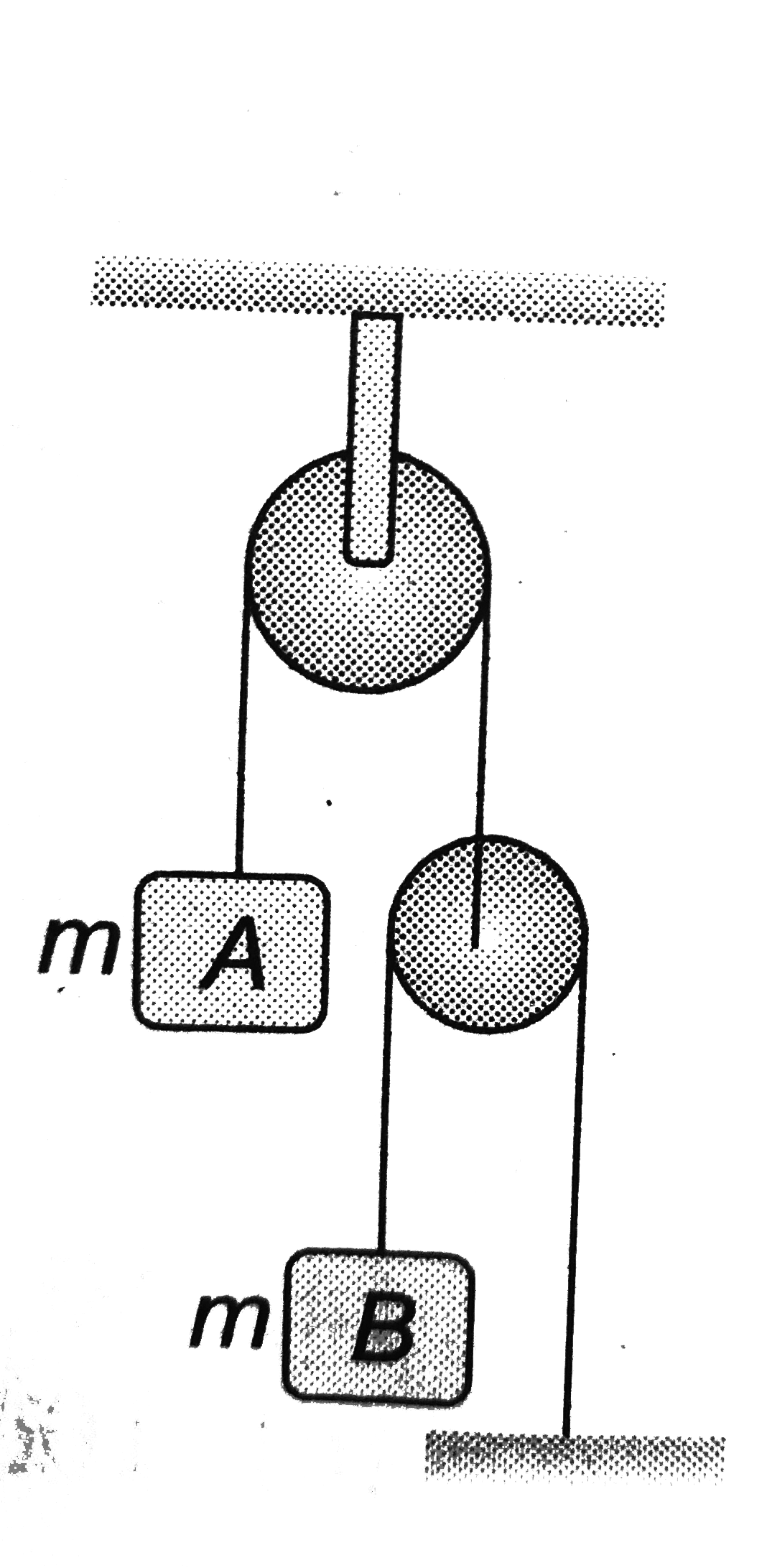 Ag3B5g2C2g2D2g5
Ag3B5g2C2g2D2g5
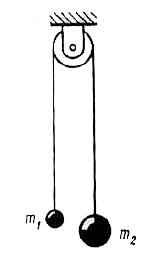
Two weights with masses m1andm2 are suspended from a thread slung over a pulley (Fig.). Find the acceleration of the system a1 the tension of the thread F and the force Fp acting on the pulley's axis. Neglect the mass of the thread and of the pulley and friction.
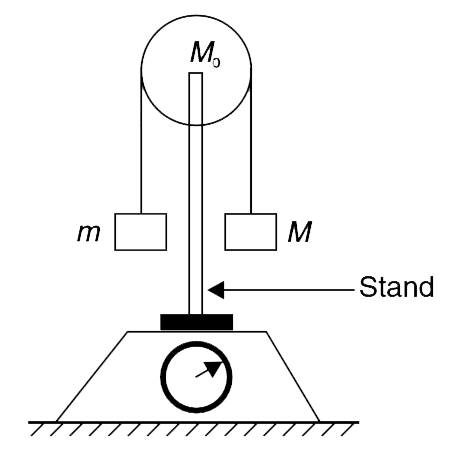
View SolutionA pulley is mounted on a stand which is placed over a weighing scale. The combined mass of the stand and the pulley is M0. A light string passes over the smooth pulley and two masses m and M (gt m) are connected to its ends (see figure). Find the reading of the scale when the two masses are left free to move.
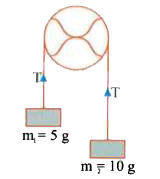
View SolutionTwo blocks m1 = 5 g and m2= 10 g are hung vertically over a light frictionless pulley as shown in figure. What is the acceleration of the masses when left free ?
View SolutionTwo mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionUSS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)

View Solution