What is the maximum vertical height to which a cricketer can throw a ball if he can throw it to a maximum horizontal distance of 160 m ?
To solve the problem of finding the maximum vertical height to which a cricketer can throw a ball given that he can throw it to a maximum horizontal distance of 160 m, we can follow these steps:
1. Understand the Problem: We need to find the maximum vertical height (H) that a ball can reach when thrown at an angle, given the maximum horizontal distance (range, R) is 160 m.
2. Use the Range Formula: The formula for the range of a projectile is given by:
R=u2sin(2θ)g
where:
- R is the range (160 m),
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 10m/s2).
3. Maximize the Range: The range is maximized when sin(2θ)=1, which occurs at θ=45∘. Therefore, we can simplify the range formula:
R=u2g
4. Calculate Initial Velocity (u): Rearranging the range formula to find u:
u2=R⋅g
Substituting the known values:
u2=160⋅10=1600
Therefore, the initial velocity u is:
u=√1600=40m/s
5. Use the Maximum Height Formula: The formula for the maximum height (H) reached by a projectile is given by:
H=u2sin2(θ)2g
Since we are using θ=45∘:
sin(45∘)=1√2
Therefore:
H=u2(1√2)22g=u2⋅122g=u24g
6. Substitute Values to Find H:
H=4024⋅10=160040=40m
Final Answer:
The maximum vertical height to which the cricketer can throw the ball is 40 meters.
R=u2sin(2θ)g
where:
- R is the range (160 m),
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity (approximately 10m/s2).
R=u2g
u2=R⋅g
Substituting the known values:
u2=160⋅10=1600
Therefore, the initial velocity u is:
u=√1600=40m/s
H=u2sin2(θ)2g
Since we are using θ=45∘:
sin(45∘)=1√2
Therefore:
H=u2(1√2)22g=u2⋅122g=u24g
H=4024⋅10=160040=40m
The maximum vertical height to which the cricketer can throw the ball is 40 meters.
Topper's Solved these Questions
Similar Questions
How much hight above the ground a mancan throw a ball if he is able to throw the same ball upto maximum distance of 60 m?
View SolutionA boy can throw a ball up to a speed of u=30m/s . He throws the ball many a times, ensuring that maximum height attained by the ball in each throw is h=20m. Calculate the maximum horizontal distance at which a ball might have landed from the point of projection. Neglect the height of the boy. [g=10m/s2]
View Solution
Knowledge Check
The angle in which a cricket ball should be hit to travel maximum horizontal distance is
A60∘ with horizontalB45∘ with horizontalC30∘ horizontalD15∘ with horizontalThe maximum vertical distance through which a person can jump on the earth (1/2)m. Then the maximum vertical distance through which he can jumb on the moon is
[Initial velocity is same is both cases and acceleration due to gravity on the moon is (1/6)th that on the earth]A2 mB12 mC6 mD3 mIf a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be- (Ball have same initial speed in each case)
Ad/2BdC2dDd/4
There is a tall cylindrical building standing in a field. Radius of the cylinder is R=8m. A boy standing at A (at a distance of 10 m from the centre of the cylindrical base of the building) knows that his friend is standing at B behind the building. The line joining A and B passes through the centre of the base of the building. Distance between A and B is 50 m. A wants to throw a ball to B but he realizes that the building is too tall and he cannot throw the ball over it. He throws the ball at a speed of 20m/s such that his friend at B has to move minimum distance to catch it.

(a) What is the minimum distance that boy at B will have to move to catch the ball?
(b) At what angle to the horizontal does the boy at A throws the ball? Assume that the ball is released and caught at same height above the ground.
[Take g=10m/s2 and sin−1(0.75)≅48.6∘
View SolutionThe maximum vertical distance through which an astronaut can jump on the earth is 0.5 m. Estimate the corresponding distance on the moon.
View SolutionThe maximum vertical distance through which a full dressed astronaut can jump on the earth is 0.5m. Estimate the maximum vertical distance through which he can jump on the motion, which has a mean density 2/3 rd that of the earth and radius one-quarter that of the earth.
View SolutionThe maximum vertical distance through which a full dressed astronaut can jump on the earth is 0.5m. Estimate the maximum vertical distance through which he can jump on the motion, which has a mean density 2/3 rd that of the earth and radius one-quarter that of the earth.
View SolutionWater is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
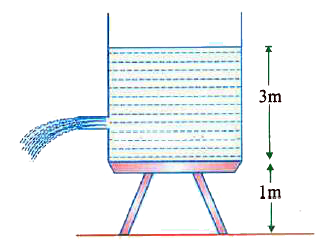
View Solution