Question

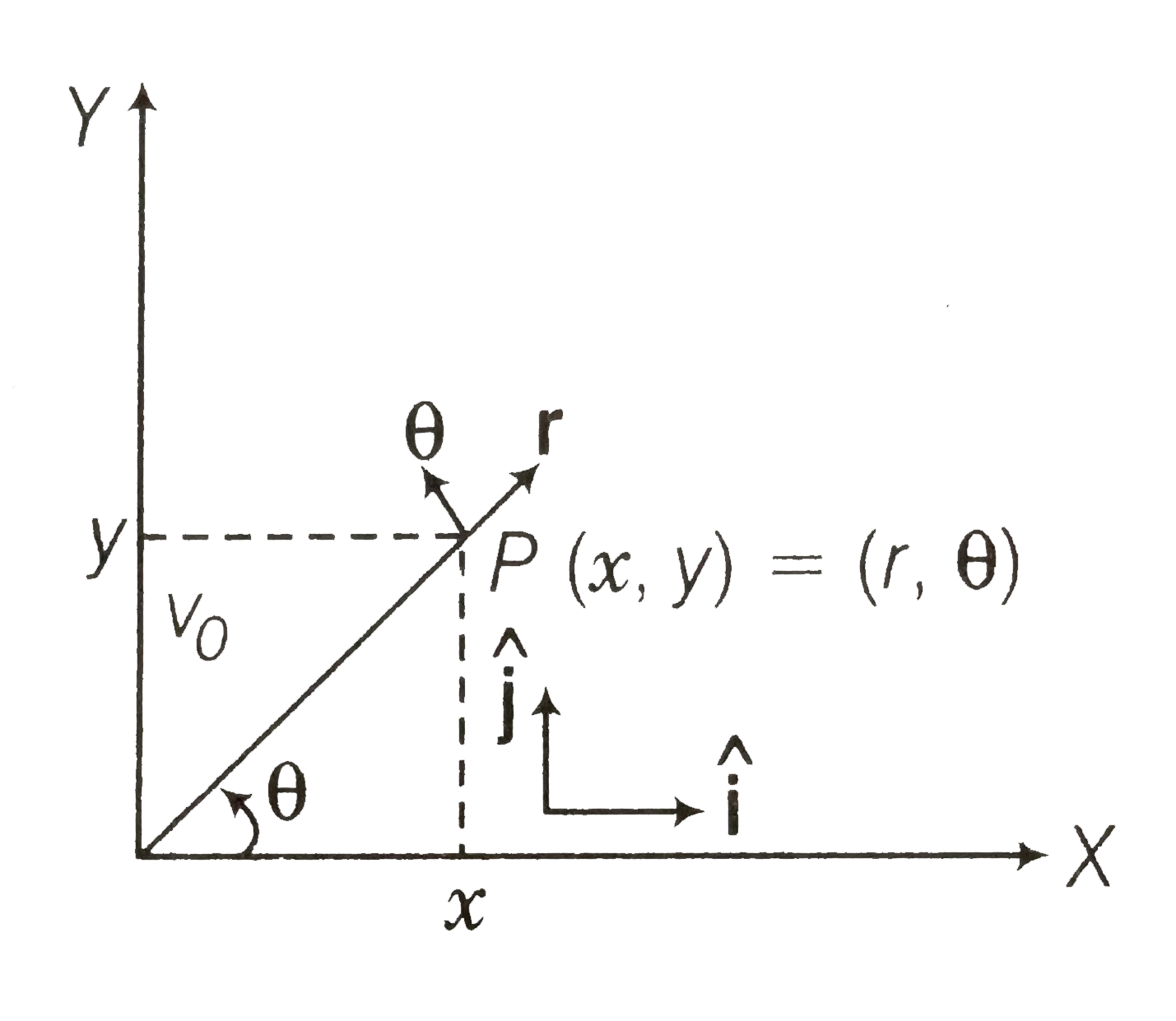
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates $A=A_x\hat{i}+A_y\hat{j}$, where $\hat{i}$ and $\hat{j}$ are unit vector along x and y-directions, respectively and $A_x$ and $A_y$ are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as $A=A_r\hat{r}+A_{\theta }\hat{\theta }$, where $\hat{r}=\frac{r}{r}=\cos \theta \hat{i}+\sin \theta \hat{j}$ and $\hat{\theta }=-\sin \theta \hat{i}+\cos \theta \hat{j}$ are unit vectors along direction in which r and $\theta$ are increasing.
(a) Express $\hat{i}$ and $\hat{j}$ in terms of $\hat{r}$ and $\hat{\theta }$.
(b) Show that both $\hat{r}$ and $\hat{\theta }$ are unit vectors and are perpendicular to each other.
(c) Show that $\frac{d}{dt}\left(\hat{r}\right)=\omega \hat{\theta }$, where $\omega =\frac{d\theta }{dt}$ and $\frac{d}{dt}\left(\hat{\theta }\right)=-\theta \hat{r}$.
(d) For a particle moving along a spiral given by $r=a\theta \hat{r}$, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.