Integrate the following: ax2+bx+c
To integrate the expression ax2+bx+c, we will follow these steps:
Step 1: Identify the expression
The expression we need to integrate is:
ax2+bx+c
Step 2: Break down the integral
We can integrate each term separately. Thus, we write:
∫(ax2+bx+c)dx=∫ax2dx+∫bxdx+∫cdx
Step 3: Integrate each term
1. Integrate ax2:
- The integral of xn is given by xn+1n+1.
- Here, n=2, so:
∫ax2dx=a⋅x2+12+1=a⋅x33=a3x3
2. Integrate bx:
- Here, n=1, so:
∫bxdx=b⋅x1+11+1=b⋅x22=b2x2
3. Integrate c:
- The integral of a constant c is:
∫cdx=c⋅x
Step 4: Combine the results
Now we combine the results of the integrals:
∫(ax2+bx+c)dx=a3x3+b2x2+cx
Step 5: Add the constant of integration
Since this is an indefinite integral, we must add a constant of integration C:
∫(ax2+bx+c)dx=a3x3+b2x2+cx+C
Final Answer:
Thus, the final result of the integration is:
a3x3+b2x2+cx+C
---
The expression we need to integrate is:
ax2+bx+c
We can integrate each term separately. Thus, we write:
∫(ax2+bx+c)dx=∫ax2dx+∫bxdx+∫cdx
1. Integrate ax2:
- The integral of xn is given by xn+1n+1.
- Here, n=2, so:
∫ax2dx=a⋅x2+12+1=a⋅x33=a3x3
- Here, n=1, so:
∫bxdx=b⋅x1+11+1=b⋅x22=b2x2
- The integral of a constant c is:
∫cdx=c⋅x
Now we combine the results of the integrals:
∫(ax2+bx+c)dx=a3x3+b2x2+cx
Since this is an indefinite integral, we must add a constant of integration C:
∫(ax2+bx+c)dx=a3x3+b2x2+cx+C
Thus, the final result of the integration is:
a3x3+b2x2+cx+C
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise20videos
Mathematical tools
- BOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Self Practice95videos
LAWS OF MOTION : FRICTION
- BOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise459videos
Mechanical Properties of fluids
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(X)=ax2+bx+c. Consider the following diagram
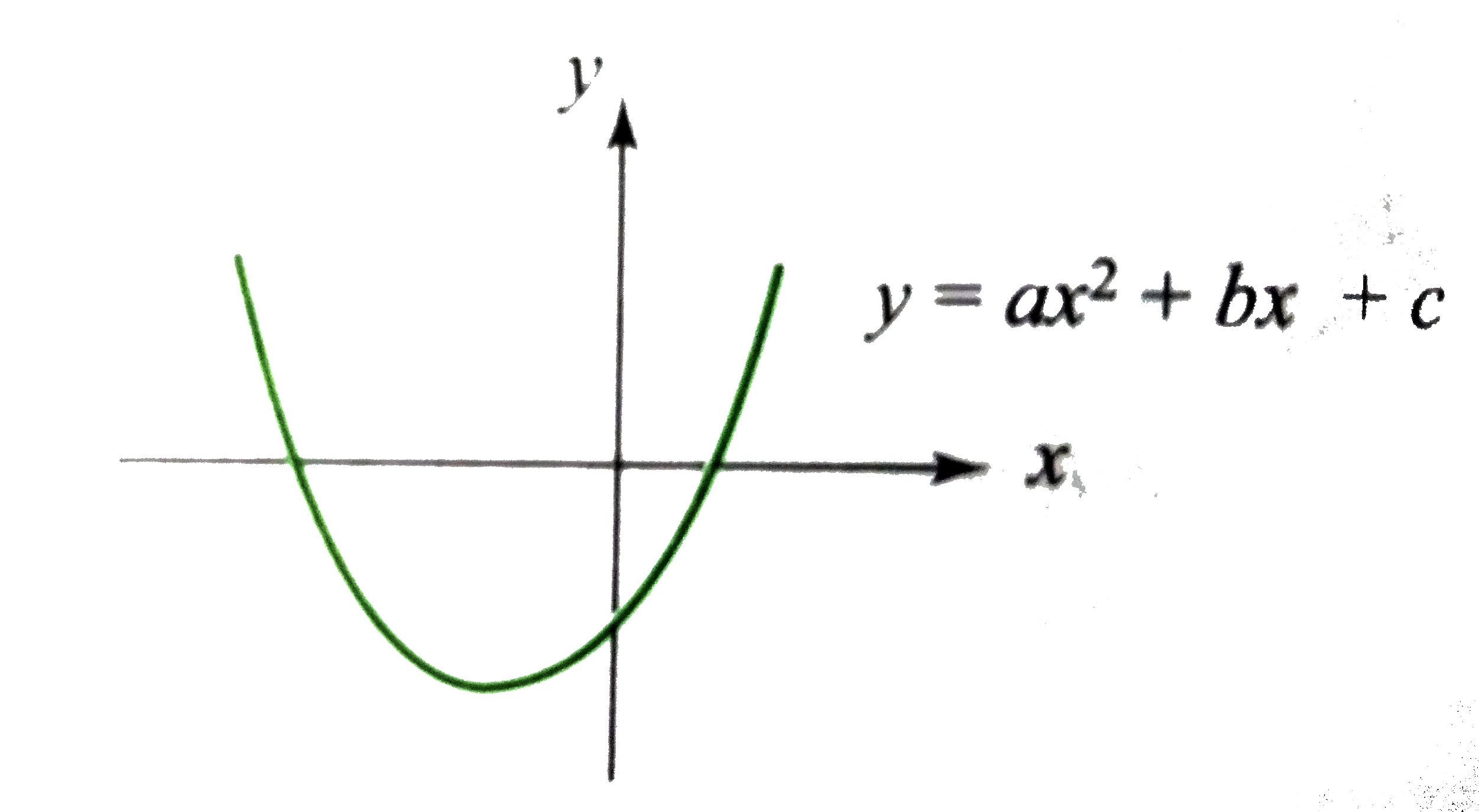 . Ac<0Bb>0Ca+b−c>0Dabc<0
. Ac<0Bb>0Ca+b−c>0Dabc<0 - Question 2 - Select One
Euler's substitution:
Integrals of the form ∫R(x,√ax2+bx+c)dx are claculated with the aid of one of the following three Euler substitutions:
i. √ax2+bx+c=t±x√aifa>0
ii. √ax2+bx+c=tx±x√cifc>0
iii. √ax2+bx+c=(x−a)tifax2+bx+c=a(x−a)(x−b) i.e., if α is real root of ax2+bx+c=0
∫xdx(√7x−10−x2)3 can be evaluated by substituting for x asAx=5+2t2t2+1Bx=5−t2t2+2Cx=2t2−53t2−1Dnone of these - Question 3 - Select One
Euler's substitution:
Integrals of the form ∫R(x,√ax2+bx+c)dx are claculated with the aid of one of the following three Euler substitutions:
i. √ax2+bx+c=t±x√aifa>0
ii. √ax2+bx+c=tx±x√cifc>0
iii. √ax2+bx+c=(x−a)tifax2+bx+c=a(x−a)(x−b) i.e., if α is real root of ax2+bx+c=0
Which of the following functions does not appear in the primitive of 11+√x2+2x+2 if t is a function of x ?Aloge|t+1|Bloge|t+2|C1t+2Dnone of these
Integral of the form √ax2+bx+cdx
View Solution∫(ax2+bx+c)dx
View SolutionWhich one of the following is the equation whose roots are respectively three times the roots of the equation ax2+bx+c=0 a)ax2+3bx+c=0 b)ax2+3bx+9c=0 c) ax2−3bx+9c=0 d)ax2+bx+3c=0
View SolutionIntegral of the form ∫(px+q)√ax2+bx+cdx
View SolutionEuler's substitution:
Integrals of the form ∫R(x,√ax2+bx+c)dx are claculated with the aid of one of the following three Euler substitutions:
i. √ax2+bx+c=t±x√aifa>0
ii. √ax2+bx+c=tx±x√cifc>0
iii. √ax2+bx+c=(x−a)tifax2+bx+c=a(x−a)(x−b) i.e., if α is real root of ax2+bx+c=0
Which of the following functions does not apear in the primitive of dxx+√x2−x+1 if t is a function of x?View Solution

