Consider an infinitely long current carrying cylindrical straight wire having radius 'a'. Then the ratio of magnetic field at distance a3 and 2a from axis of wire is.
2/3
1/2
3/2
2
The correct Answer is:1
To solve the problem of finding the ratio of the magnetic field at distances a3 and 2a from the axis of an infinitely long current-carrying cylindrical wire, we can follow these steps:
Step 1: Understand the Magnetic Field Inside and Outside the Wire
For a long straight wire carrying current I:
- Inside the wire (for r<a), the magnetic field B is given by:
B=μ0I2πa2r
where r is the distance from the center of the wire.
- Outside the wire (for r≥a), the magnetic field B is given by:
B=μ0I2πr
Step 2: Calculate the Magnetic Field at r=a3
Since a3<a, we use the formula for the magnetic field inside the wire:
B1=μ0I2πa2(a3)=μ0I2πa2⋅a3=μ0I6πa
Step 3: Calculate the Magnetic Field at r=2a
Since 2a>a, we use the formula for the magnetic field outside the wire:
B2=μ0I2π(2a)=μ0I4πa
Step 4: Find the Ratio of the Magnetic Fields
Now, we can find the ratio of B1 to B2:
Ratio=B1B2=μ0I6πaμ0I4πa=1/61/4=46=23
Final Answer
Thus, the ratio of the magnetic field at a distance a3 from the axis of the wire to the magnetic field at a distance 2a is:
B1B2=23
For a long straight wire carrying current I:
- Inside the wire (for r<a), the magnetic field B is given by:
B=μ0I2πa2r
where r is the distance from the center of the wire.
- Outside the wire (for r≥a), the magnetic field B is given by:
B=μ0I2πr
Since a3<a, we use the formula for the magnetic field inside the wire:
B1=μ0I2πa2(a3)=μ0I2πa2⋅a3=μ0I6πa
Since 2a>a, we use the formula for the magnetic field outside the wire:
B2=μ0I2π(2a)=μ0I4πa
Now, we can find the ratio of B1 to B2:
Ratio=B1B2=μ0I6πaμ0I4πa=1/61/4=46=23
Thus, the ratio of the magnetic field at a distance a3 from the axis of the wire to the magnetic field at a distance 2a is:
B1B2=23
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
A current of 2 amp. flows in a long, straight wire of radius 2mm. The intensity of magnetic field on the axis of the wire is
View SolutionIn figure two infinitely long current carrying wires are shown . If resultant magnetic field at point A is zero. Then determine current I1 .
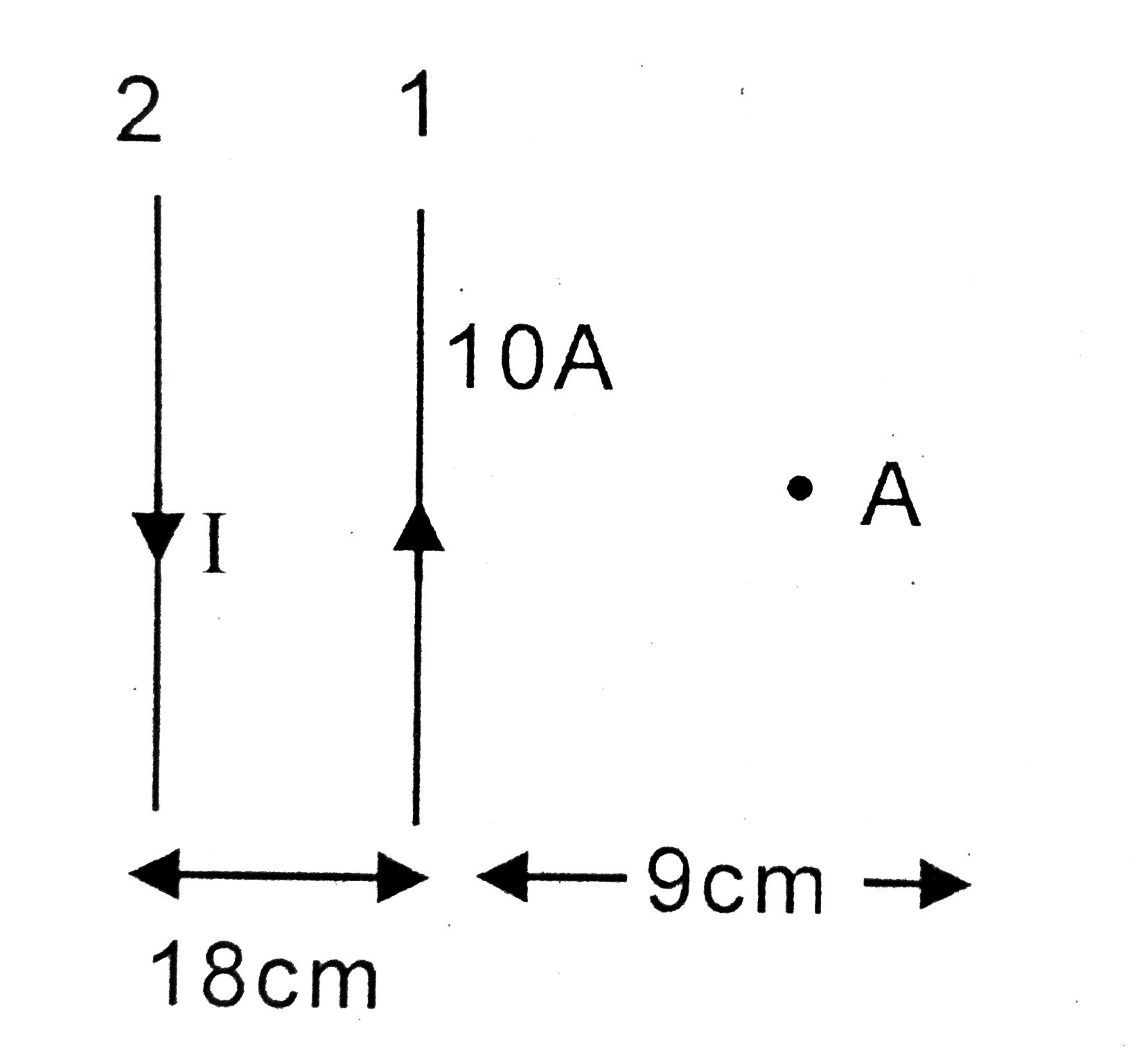
View SolutionAssertion three infinitely long current carrying wires have equal currents and they are equally spaced. The magnitude of magnetic force on all three is same.
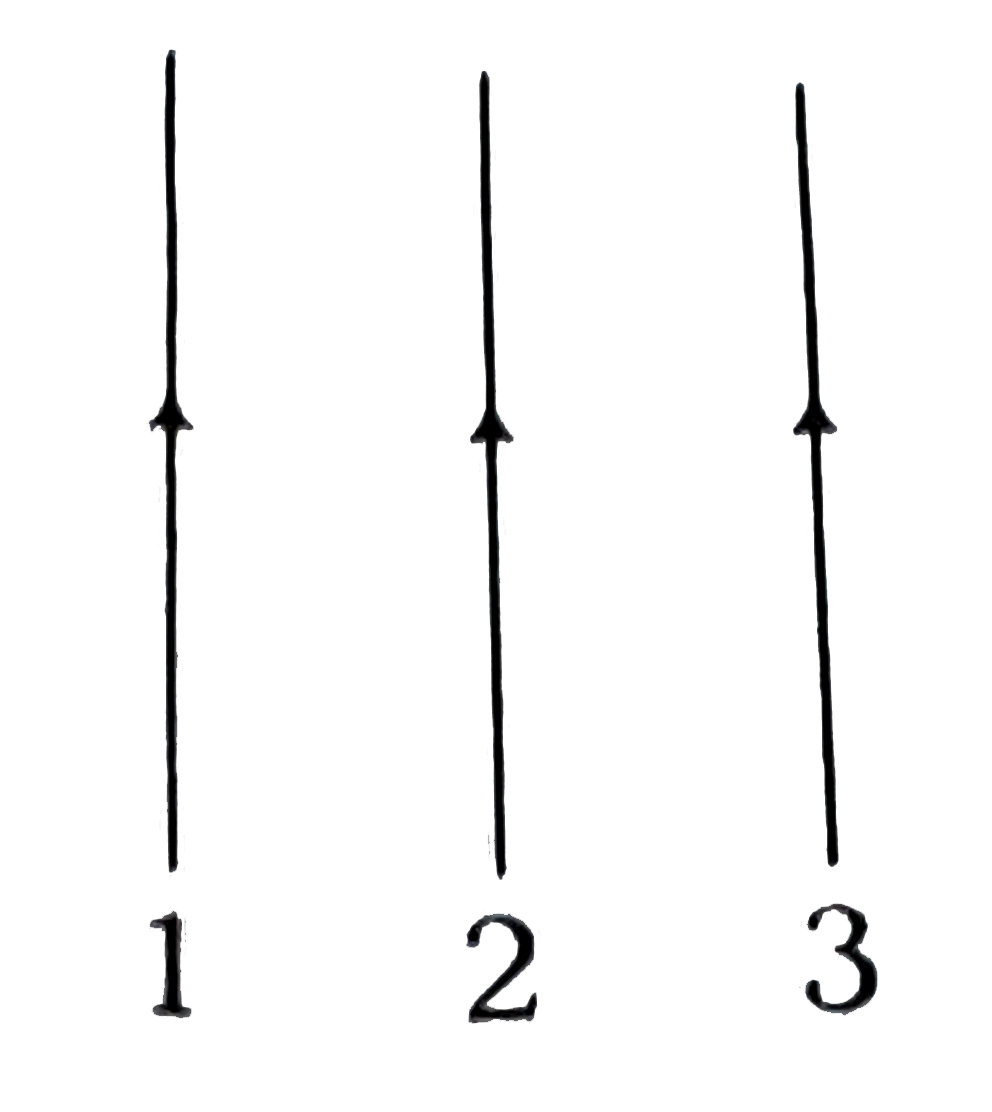
Reason Net force on wire-2 is zero.
View SolutionA long straight wire carrying current i=10A lies along y-axis. Find the magnetic field at P(3cm, 2cm,4cm).

View SolutionA long staright wire of radius a carries a steady current I. The curent is unifromly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
View SolutionAn electric current passes through a long straight copper wire. At a distance of 5 cm from the straight wire, the magnetic field is B. What is the magnetic field at a distance of 20 cm from the wire ?
View SolutionA long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
View Solution

