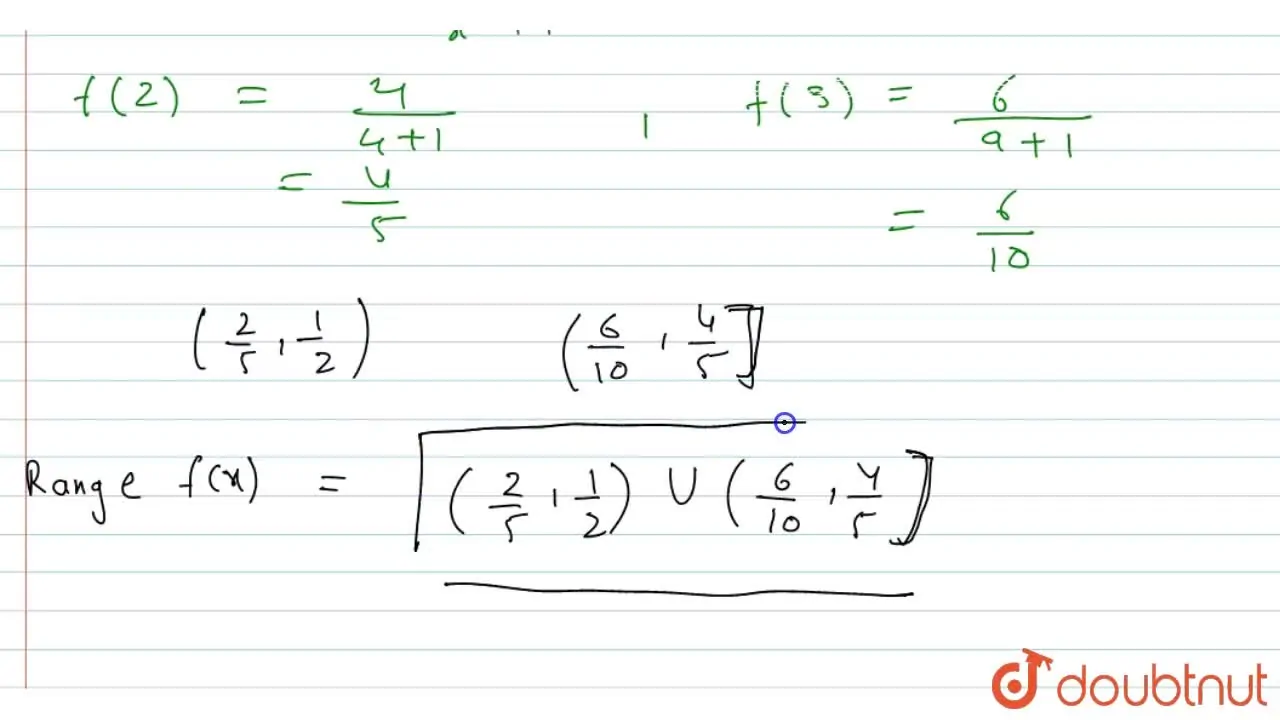Let then range of f(x) is (where [ . ] denotes greatest integer function)
The correct Answer is:B
NA
Similar Questions
Let f(x)=[|x|] where [.] denotes the greatest integer function, then f'(−1) is
View SolutionThe range of the function f(x)=2+x−[x−3] is, (where [.] denotes greatest integer function):
View SolutionThe function, f(x)=[|x|]−|[x]| where [] denotes greatest integer function:
View SolutionLet f(x)=[9x−3x+1] for all x∈(−∞,1), then the range of f(x) is, ([.] denotes the greatest integer function).
View SolutionLet f(x)=[9x−3x+1] for all x∈(−∞,1), then the range of f(x) is, ([.] denotes the greatest integer function).
View SolutionIf f(x)=2[x]+cosx, then f:R→R is: (where [ ] denotes greatest integer function)
View SolutionIf f(x)=sin−1x and g(x)=[sin(cosx)]+[cos(sinx)], then range of f(g(x)) is (where [⋅] denotes greatest integer function)
View SolutionThe range of f(x)=2+x−[x]1−x+[x].where [ ] denotes the greatest integer function is
View Solutionf(x)=sin−1[log2(x22)] where [ . ] denotes the greatest integer function.
View SolutionRange of f(x)=sin−1[x−1]+2cos−1[x−2] ([.] denotes greatest integer function)
View Solution