Consider the function f(x)=|x−2|+|x−5|,x∈R . Statement 1: f'(4)=0 Statement 2: f is continuous in [2,5], differentiable in (2,5)andf(2)=f(5). (1) Statement 1 is false, statement 2 is true (2) Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1 (3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1 (4) Statement 1 is true, statement 2 is false
To solve the problem, we need to analyze the function f(x)=|x−2|+|x−5| and evaluate the two statements provided.
Step 1: Analyze the function
The function f(x) is defined using absolute values, which means we need to consider different cases based on the values of x.
1. Case 1: x<2
f(x)=−(x−2)−(x−5)=−x+2−x+5=−2x+7
2. Case 2: 2≤x<5
f(x)=(x−2)−(x−5)=x−2+5−x=3
3. Case 3: x≥5
f(x)=(x−2)+(x−5)=x−2+x−5=2x−7
Thus, we can summarize the function as:
f(x)=⎧⎨⎩−2x+7if x<23if 2≤x<52x−7if x≥5
Step 2: Check the statements
Statement 1: f′(4)=0
Since 4 is in the interval (2,5), we use the case where 2≤x<5:
f(x)=3
The derivative of a constant function is:
f′(x)=0for 2<x<5
Thus, f′(4)=0 is true.
Statement 2:
- Continuity in (2,5): The function is constant (3) in the interval (2,5), so it is continuous.
- Differentiability in (2,5): The function is constant in this interval, hence differentiable.
- Equality f(2)=f(5):
f(2)=3andf(5)=3
So f(2)=f(5) is also true.
Thus, Statement 2 is true.
Conclusion
Both statements are true. However, Statement 2 does not serve as a correct explanation for Statement 1 since Statement 1 is true due to the nature of the function being constant in the interval.
The correct option is:
(3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
The function f(x) is defined using absolute values, which means we need to consider different cases based on the values of x.
f(x)=−(x−2)−(x−5)=−x+2−x+5=−2x+7
f(x)=(x−2)−(x−5)=x−2+5−x=3
f(x)=(x−2)+(x−5)=x−2+x−5=2x−7
f(x)=⎧⎨⎩−2x+7if x<23if 2≤x<52x−7if x≥5
f(x)=3
The derivative of a constant function is:
f′(x)=0for 2<x<5
Thus, f′(4)=0 is true.
- Continuity in (2,5): The function is constant (3) in the interval (2,5), so it is continuous.
- Differentiability in (2,5): The function is constant in this interval, hence differentiable.
- Equality f(2)=f(5):
f(2)=3andf(5)=3
So f(2)=f(5) is also true.
Both statements are true. However, Statement 2 does not serve as a correct explanation for Statement 1 since Statement 1 is true due to the nature of the function being constant in the interval.
(3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
Topper's Solved these Questions
Similar Questions
Consider the function f(x)=|x−2|+|x−5|,c∈R.
Statement 1: f'(4)=0
Statement 2: f is continuous in [2,5], differentiable in (2,5),
View SolutionStatement 1: n∑r=0(r+1)ncr=(n+2)2n−1.
Statement 2: n∑r=0(r+1)ncr=(1+x)n+nx(1+x)n−1.
(1) Statement 1 is false, Statement 2 is true.
(2) Statement 1 is true, Statement 2 is true, Statement 2 is a correct explanation for Statement 1
(3) Statement 1 is true, Statement 2 is true; Statement 2 is not a correct explanation for Statement 1.
(4) Statement 1 is true, Statement 2 is false.
View SolutionLet a, b R be such that the function f given by f(x)=ln|x|+bx2+ax,x≠0 has extreme values at x=1 and x=2 . Statement 1: f has local maximum at x=1 and at x=2 . Statement 2: a=12andb=−14 (1) Statement 1 is false, statement 2 is true (2) Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1 (3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1 (4) Statement 1 is true, statement 2 is false
View SolutionLet x1,x2,......,xn be n observations, and let ¯x be their arithematic mean and σ2 be their variance. Statement 1: Variance of 2x1,2x2,......,2xnis4σ2 . Statement 2: Arithmetic mean of 2x1,2x2,......,2xnis4x . (1) Statement 1 is false, statement 2 is true (2) Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1 (3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1 (4) Statement 1 is true, statement 2 is false
View SolutionStatement 1: An equation of a common tangent to the parabola y2=16√3x and the ellipse 2x2+y2=4isy=2x+2√3 . Statement 2: If the line y=mx+4√3m,(m≠0) is a common tangent to the parabola y2=16√3x and the ellipse 2x2+y2=4 , then m satisfies m4+2m2=24 . (1) Statement 1 is false, statement 2 is true (2) Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1 (3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1 (4) Statement 1 is true, statement 2 is false
View SolutionStatement 1: The sum of the series 1+(1+2+4)+(4+6+9)+(9+12+16)+...... +(361+380+400)is8000 . Statement 2: n∑k=1(k3−(k−1)3)=n3 for any natural number n. (1) Statement 1 is false, statement 2 is true (2) Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1 (3) Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1 (4) Statement 1 is true, statement 2 is false
View SolutionStatement-1: In naphthalene all C-C bonds are equal
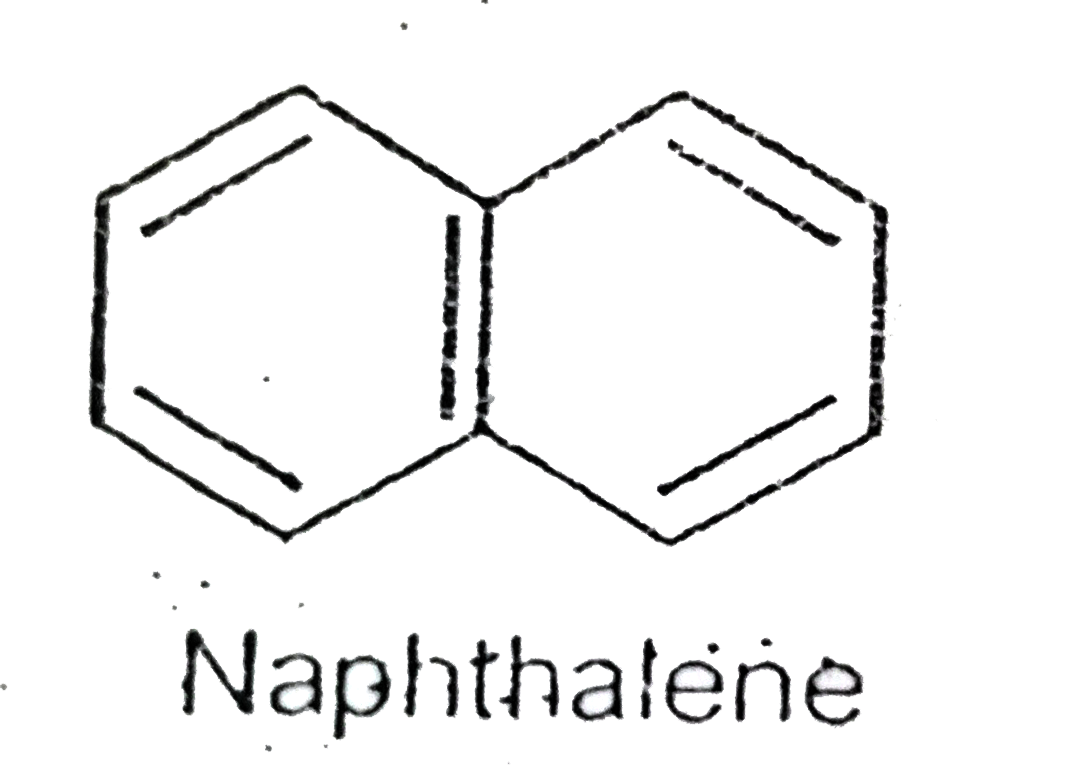
and
Statement-2: Like benzene naphthalene is also aromatic.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
(b) Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
View SolutionStatement-1: p-Nitroaniline is more polar than nitrobenzene
and
Statement-2: Nitro group has -M effect.
(a) Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1
(b) Statement-1 is true, Statement-2 is true, Statement-2 is not a correct explanation for Statement -1
(c) Statement -1 is true, Statement -2 is false
(d) Statement -1 is false, Statement -2 is true
View SolutionLet A be a 2×2 matrix with real entries. Let I be the 2×2 identity matrix. Denote by tr (A), the sum of diagonal entries of A. Assume that A2=I . Statement 1: If A≠I and A≠−I , then det A=−1 . Statement 2: If A≠I and A≠−I , then tr(A)≠0 . (1) Statement 1 is false, Statement (2)(3)−2(4) is true (6) Statement 1 is true, Statement (7)(8)−2(9) (10) is true, Statement (11)(12)−2(13) is a correct explanation for Statement 1 (15) Statement 1 is true, Statement (16)(17)−2(18) (19) is true; Statement (20)(21)−2(22) is not a correct explanation for Statement 1. (24) Statement 1 is true, Statement (25)(26)−2(27) is false.
View SolutionLet f(x)=x|x|andg(x)=sinx∈x
Statement 1 : gof is differentiable at x=0 and its derivative is continuous at that point
Statement 2: gof is twice differentiable at x=0
(1) Statement1 is true, Statement2 is true, Statement2 is a correct explanation for statement1
(2) Statement1 is true, Statement2 is true; Statement2 is not a correct explanation for statement1.
(3) Statement1 is true, statement2 is false.
(4) Statement1 is false, Statement2 is true
View Solution

