One mole of an ideal monoatomic gas at 27∘C is subjected to a reversible isoentropic compression until the temperature reached to 327∘C. If the initial pressure was 1.0atm, then find the value of ln P2
( Given :ln2=0.7)
1.75 atm
0.176 atm
1.0395 atm
2.0 atm
The correct Answer is:A
To solve the problem of finding the value of lnP2 for a monoatomic ideal gas undergoing isoentropic compression, we can follow these steps:
Step 1: Understand the Process
The process is isoentropic, meaning that the entropy change ΔS=0. For an ideal gas, the relationship between temperature and pressure during an isoentropic process can be expressed using the formula:
ΔS=nCplnT2T1+nRlnP1P2=0
Where:
- n is the number of moles of gas (1 mole in this case),
- Cp is the molar heat capacity at constant pressure,
- R is the universal gas constant,
- T1 and T2 are the initial and final temperatures,
- P1 and P2 are the initial and final pressures.
Step 2: Identify Given Values
- Initial temperature T1=27∘C=300K (after converting Celsius to Kelvin),
- Final temperature T2=327∘C=600K,
- Initial pressure P1=1.0atm,
- For a monoatomic ideal gas, Cp=52R.
Step 3: Substitute Values into the Equation
Substituting the known values into the isoentropic equation:
0=nCplnT2T1+nRlnP1P2
This simplifies to:
0=1⋅52Rln600300+1⋅Rln1P2
This can be rewritten as:
0=52Rln2+Rln1P2
Step 4: Cancel R and Rearrange
Since R is a common factor, we can cancel it from both sides:
0=52ln2+ln1P2
Rearranging gives:
ln1P2=−52ln2
Step 5: Solve for lnP2
Taking the negative of both sides:
lnP2=52ln2
Now substituting ln2=0.7:
lnP2=52×0.7=3.52=1.75
Final Answer
Thus, the value of lnP2 is:
lnP2=1.75
The process is isoentropic, meaning that the entropy change ΔS=0. For an ideal gas, the relationship between temperature and pressure during an isoentropic process can be expressed using the formula:
ΔS=nCplnT2T1+nRlnP1P2=0
Where:
- n is the number of moles of gas (1 mole in this case),
- Cp is the molar heat capacity at constant pressure,
- R is the universal gas constant,
- T1 and T2 are the initial and final temperatures,
- P1 and P2 are the initial and final pressures.
- Initial temperature T1=27∘C=300K (after converting Celsius to Kelvin),
- Final temperature T2=327∘C=600K,
- Initial pressure P1=1.0atm,
- For a monoatomic ideal gas, Cp=52R.
Substituting the known values into the isoentropic equation:
0=nCplnT2T1+nRlnP1P2
This simplifies to:
0=1⋅52Rln600300+1⋅Rln1P2
This can be rewritten as:
0=52Rln2+Rln1P2
Since R is a common factor, we can cancel it from both sides:
0=52ln2+ln1P2
Rearranging gives:
ln1P2=−52ln2
Taking the negative of both sides:
lnP2=52ln2
Now substituting ln2=0.7:
lnP2=52×0.7=3.52=1.75
Thus, the value of lnP2 is:
lnP2=1.75
Topper's Solved these Questions
Similar Questions
One mole of an ideal gas at 25∘C is subjected to expand reversible ten times of its initial volume. The change in entropy of expansion is
View SolutionOne mole of and ideal monoatomic gas is compressed isothermally in a rigid vessel to double its pressure at room temperature, 27∘C . The work done on the gas will be :
View Solution
Knowledge Check
One mole of an ideal monoatomic gas at temperature T0 expands slowly according to the law pV = constant. If the final temperature is 2T0, heat supplied to the gas is
A2RT0BRToC32RT0D12RT0One mole of an ideal monatomic gas at temperature T0 expands slowly according to the law PV=constant.If the final temperature is 2T0, heat supplied to the gas is
A2RT0BRT0C32RT0D12RT0One mole of an ideal monoatomic gas at temperature T0 expands slowly according to the law pV = constant. If the final temperature is 2T0, heat supplied to the gas is
Aa.2RT0Bb.RT0Cc.32RT0Dd.12RT0
At 2 atm pressure the value of xm will be : (log 2 = 0.3010)
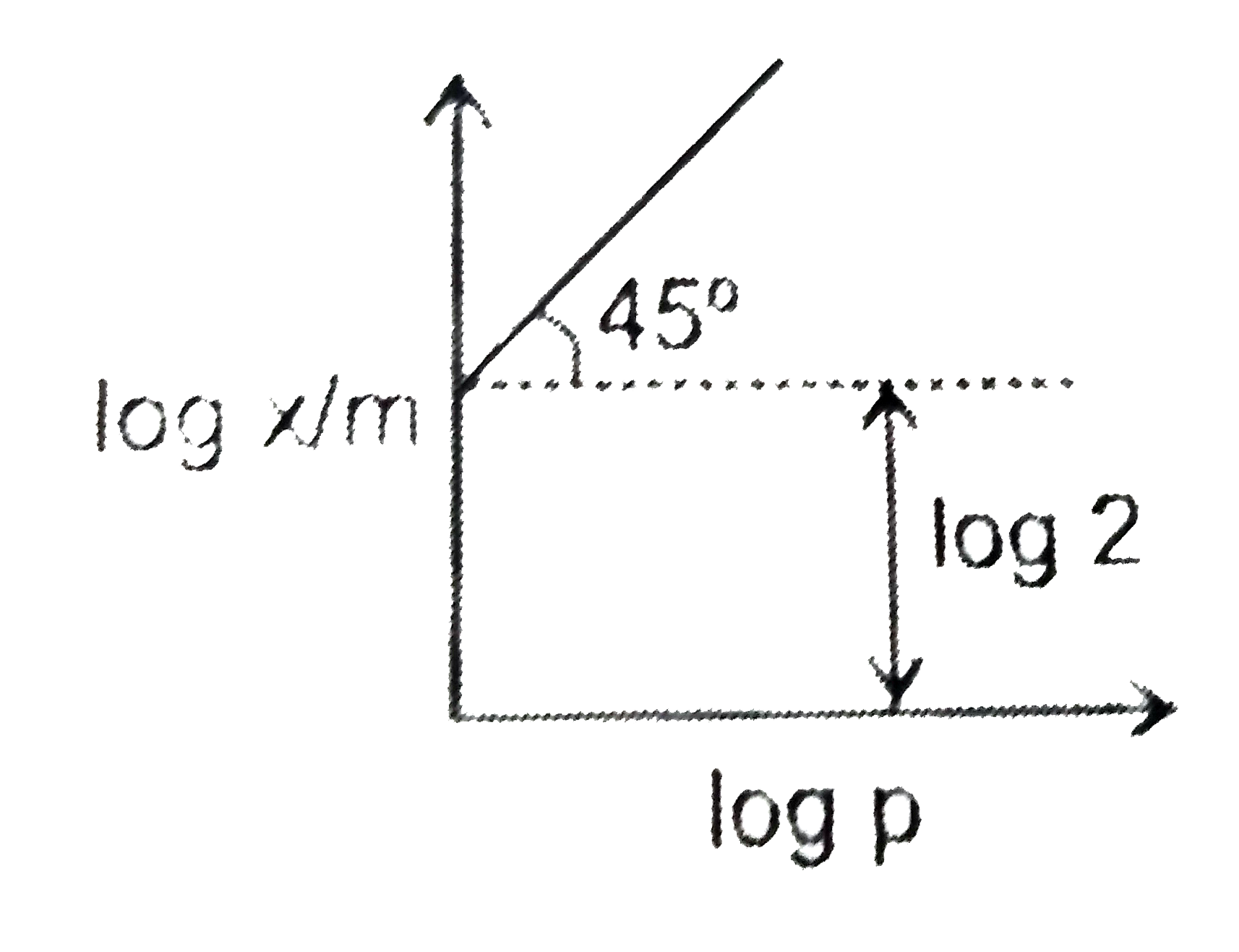
View SolutionFind the value of log2(17log70.125).
View Solution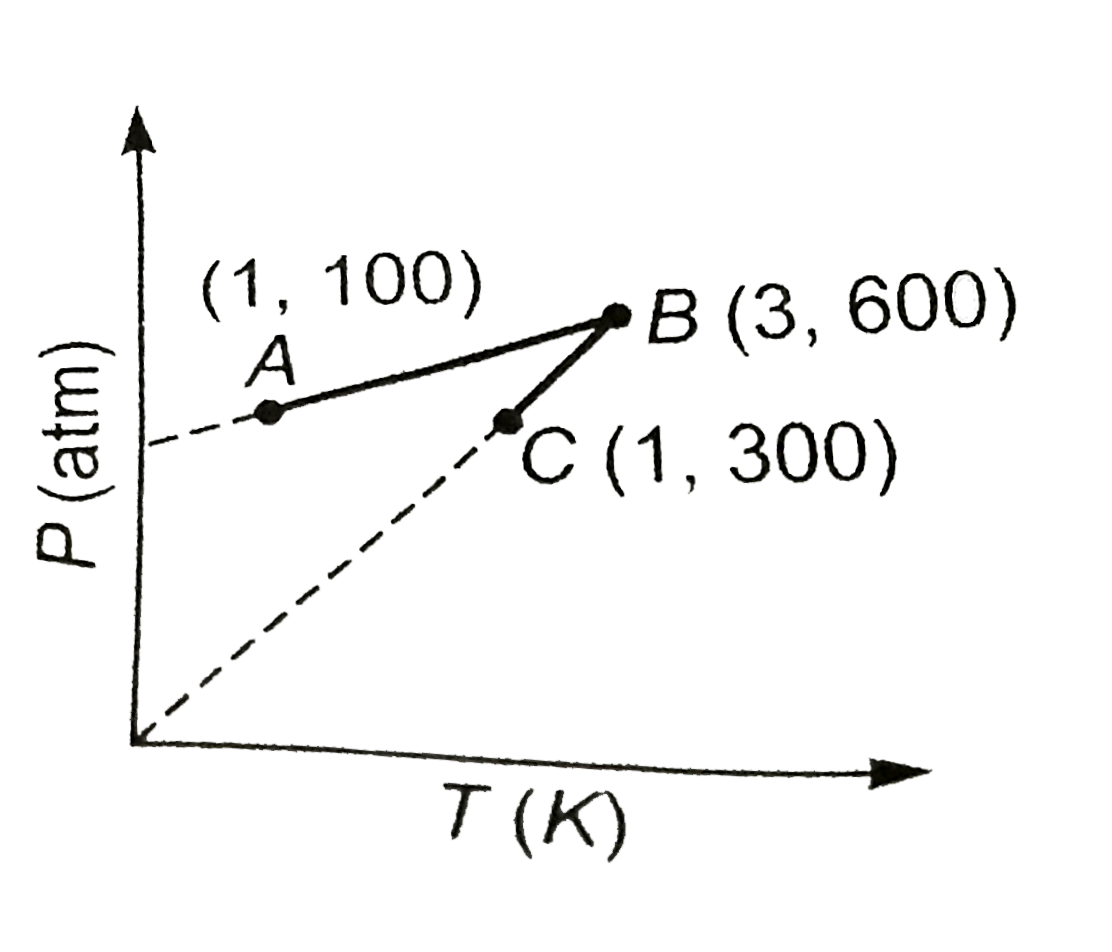
One mole of an ideal gas is subjected to a two step reversible process (A-B and B-C). The pressure at A and C is same. Mark the correct statement(s) :
View SolutionOne mole of an ideal monoatomic gas at temperature T0 expands slowly according to the law pV = constant. If the final temperature is 2T0, heat supplied to the gas is
View SolutionOne mole of an ideal monoatomic gas at 27∘ C expands adiabatically against constant external pressure of 1 atm from volume of 10 dm3 to a volume of 20dm3.
View Solution
