Consider a p-n junction diode having the characteristic i=i0(eeV/kT−1)where i0=20(μ)A. The diode is operated at T=300K. (a) Find the current through the diode when a voltage of 300 mV is applied across it in forward bias, (b) At what voltage does the current double?
To solve the problem step by step, we will break it down into two parts as per the question.
Part (a): Find the current through the diode when a voltage of 300 mV is applied.
1. Identify the given values:
- I0=20μA=20×10−6A
- Voltage V=300mV=300×10−3V
- Temperature T=300K
- Boltzmann constant k=1.38×10−23J/K
- Charge of an electron e=1.6×10−19C
2. Write the diode current equation:
i=I0(eeVkT−1)
3. Substitute the known values into the equation:
i=20×10−6⎛⎝e(1.6×10−19)(300×10−3)(1.38×10−23)(300)−1⎞⎠
4. Simplify the exponent:
- Calculate eVkT:
(1.6×10−19)(300×10−3)(1.38×10−23)(300)=(1.6×10−19)(0.3)(1.38×10−23)(300)=4.8×10−204.14×10−21≈11.6
5. Calculate the current:
i=20×10−6(e11.6−1)
- Calculate e11.6:
e11.6≈108467.17
- Substitute back:
i≈20×10−6×(108467.17−1)≈20×10−6×108467.17≈2.17A
Part (b): At what voltage does the current double?
1. Set the new current:
- New current i=2×2.17A=4.34A
2. Use the diode equation again:
4.34=20×10−6(eeVkT−1)
3. Rearranging the equation:
eeVkT−1=4.3420×10−6
eeVkT=4.3420×10−6+1≈217000+1≈217000
4. Take the natural logarithm:
eVkT=ln(217000)
- Calculate ln(217000)≈12.206
5. Solve for V:
V=12.206⋅kTe=12.206⋅(1.38×10−23)(300)1.6×10−19
- Calculate:
V≈12.206⋅4.14×10−211.6×10−19≈0.318V=318mV
Final Answers:
- (a) The current through the diode when a voltage of 300 mV is applied is approximately 2.17 A.
- (b) The voltage at which the current doubles is approximately 318 mV.
- I0=20μA=20×10−6A
- Voltage V=300mV=300×10−3V
- Temperature T=300K
- Boltzmann constant k=1.38×10−23J/K
- Charge of an electron e=1.6×10−19C
i=I0(eeVkT−1)
i=20×10−6⎛⎝e(1.6×10−19)(300×10−3)(1.38×10−23)(300)−1⎞⎠
- Calculate eVkT:
(1.6×10−19)(300×10−3)(1.38×10−23)(300)=(1.6×10−19)(0.3)(1.38×10−23)(300)=4.8×10−204.14×10−21≈11.6
i=20×10−6(e11.6−1)
- Calculate e11.6:
e11.6≈108467.17
- Substitute back:
i≈20×10−6×(108467.17−1)≈20×10−6×108467.17≈2.17A
- New current i=2×2.17A=4.34A
4.34=20×10−6(eeVkT−1)
eeVkT−1=4.3420×10−6
eeVkT=4.3420×10−6+1≈217000+1≈217000
eVkT=ln(217000)
- Calculate ln(217000)≈12.206
V=12.206⋅kTe=12.206⋅(1.38×10−23)(300)1.6×10−19
- Calculate:
V≈12.206⋅4.14×10−211.6×10−19≈0.318V=318mV
- (a) The current through the diode when a voltage of 300 mV is applied is approximately 2.17 A.
- (b) The voltage at which the current doubles is approximately 318 mV.
Topper's Solved these Questions
- SEMICONDUCTOR AND SEMICONDUCTOR DEVICESBOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - Question for short answer
11 Videos
- SEMICONDUCTOR AND SEMICONDUCTOR DEVICESBOOK - HC VERMA ENGLISHCHAPTER - SEMICONDUCTOR AND SEMICONDUCTOR DEVICESEXERCISE - objective II
8 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
- SPEED OF LIGHTBOOK - HC VERMA ENGLISHCHAPTER - SPEED OF LIGHTEXERCISE - Question for short Answer
5 Videos
Similar Questions
In a p−n junction diode, the currect I can expressed as I=I0exp(eV2kBT−1) where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, KB is the Boltzmann constant (8.6×10−5eV/K) and T is the absolute temperature. If for a given diode Io=5×10−12A and T=300K, then
(a) What will be the forward current at a formward voltage of 0.6V ?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7V ?
( c) What is the dynamic resistance ?
(d) What will be current if reverse bias voltage changes from 1V to 2V ?
View SolutionThe i-V characteristic of a p-n junction diode is shown in figure.Find the approximate dynamic resistance of the p-n junction when (a) a forward bias of 1 volt is applied ,(b) a forward bias of 2 volt is applied is applied .

View Solution
Knowledge Check
When the voltage drop across a p.n junction diode is increased from 0.65V to 0.70V, the change in the diode current is 5mA. What is the dynamic resistance of the diode?
A5ΩB10ΩC20ΩD25Ω
The current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionThe current through an inductor of 1H is given by i=3tsint. Find the voltage across the inductor.
View SolutionA PN junction diode when forward biased has a drop of 0.5V which is assumed to be independent of current. The current in excess of 10mA through the diode produces large joule heating which damages the diode. If we want to use a 1.5V battery to forward bias the diode, the resistor used in series with the diode so that the maximum current does not exceed 5mA is.
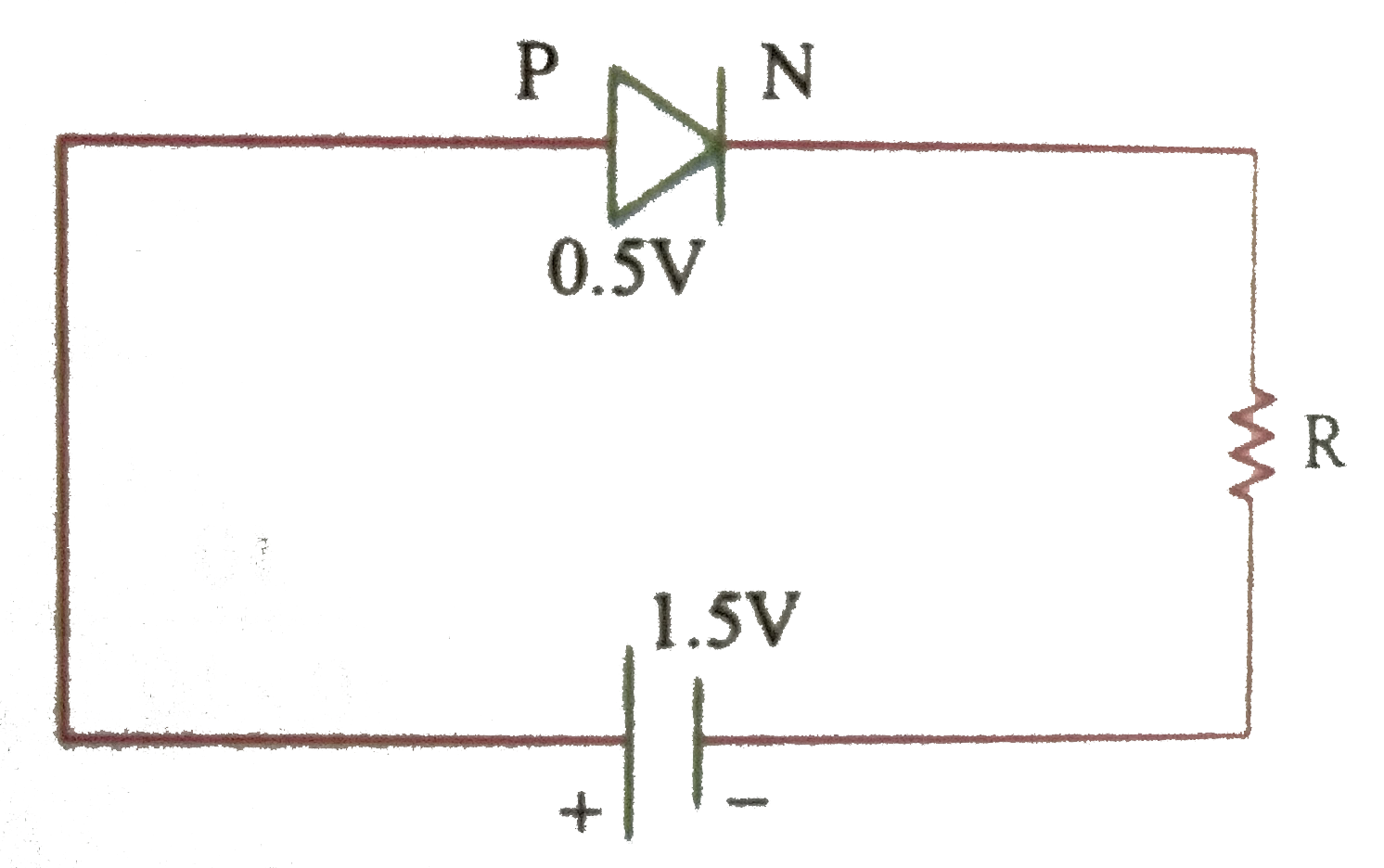 .
.
View SolutionA P−N junction diode can withstand currents up to 10mA. Under forward bias, The diode has a potential drop of 0.5V across it which is assumed to be independent of current. The maximum voltage of the battery used to forward bias the diode when a resistance of 200Ω is connected in series with it is
View SolutionWhen the voltage drop across a p-n junction is increased from 0.80 V to 0.82 V, the change in the diode current is 20 mA. What is the dynamic resistance of the diode ?
View SolutionWhen the forwward bias voltage of a diode is changed from 0.6 V to 0.7 V the current changes from 5 mA to 15 mA. Then its forward bias resistance is
View SolutionA 1.00mH inductor and a 1.00μF capacitor are connected in series. The current in the circuit is described by i=20t, where t, is in second and i is in ampere. The capacitor initially has no charge. Determine
(a) the voltage across the inductor as a function of time,
(b) the voltage across the capacitor as a function of time,
(c) the time when the energy stored in the capacitor first exceeds that in the inductor.
View Solution
