Suppose in an imginary world the angular momentum is quantized to be even integral multiples of . What is the longest possible wavelenght emitted by hydrogen atoms in visible range in such a world according to Bohr's model?
The correct Answer is:D
To find the longest possible wavelength emitted by hydrogen atoms in the visible range in an imaginary world where angular momentum is quantized to be even integral multiples of h2π, we can follow these steps:
Step 1: Understand the quantization of angular momentum
In this imaginary world, the angular momentum L of an electron in a hydrogen atom is given by:
L=nh2π
where n is an even integer (2, 4, 6, ...).
Step 2: Determine the energy levels
The energy of the electron in the nth level of hydrogen is given by:
En=−13.6eVn2
Since n can only take even values, the possible values for n are 2, 4, 6, etc.
Step 3: Calculate the energy difference for transitions
To find the longest wavelength emitted, we need to find the smallest energy difference between two energy levels. The smallest energy difference occurs between consecutive levels. Therefore, we will consider n1=2 and n2=4.
The energy difference ΔE between these two levels is:
ΔE=En1−En2=(−13.622)−(−13.642)
Calculating this gives:
ΔE=−13.64+13.616=−3.4+0.85=−2.55eV
Step 4: Relate energy to wavelength
Using the relation between energy and wavelength:
E=hcλ
we can rearrange this to find the wavelength:
λ=hcE
Substituting the values of h and c:
- h=4.135667696×10−15eV s
- c=3×108m/s
Using E=2.55eV:
λ=1242eV nm2.55eV≈487.05nm
Step 5: Conclusion
The longest possible wavelength emitted by hydrogen atoms in the visible range in this imaginary world is approximately:
λ≈487nm
In this imaginary world, the angular momentum L of an electron in a hydrogen atom is given by:
L=nh2π
where n is an even integer (2, 4, 6, ...).
The energy of the electron in the nth level of hydrogen is given by:
En=−13.6eVn2
Since n can only take even values, the possible values for n are 2, 4, 6, etc.
To find the longest wavelength emitted, we need to find the smallest energy difference between two energy levels. The smallest energy difference occurs between consecutive levels. Therefore, we will consider n1=2 and n2=4.
ΔE=En1−En2=(−13.622)−(−13.642)
Calculating this gives:
ΔE=−13.64+13.616=−3.4+0.85=−2.55eV
Using the relation between energy and wavelength:
E=hcλ
we can rearrange this to find the wavelength:
λ=hcE
Substituting the values of h and c:
- h=4.135667696×10−15eV s
- c=3×108m/s
λ=1242eV nm2.55eV≈487.05nm
The longest possible wavelength emitted by hydrogen atoms in the visible range in this imaginary world is approximately:
λ≈487nm
Topper's Solved these Questions
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Short Answer
Explore 10 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Obejective - II
Explore 5 Videos
- ALTERNATING CURRENTBook:HC VERMA ENGLISHChapter:ALTERNATING CURRENTExercise:Short answer
Explore 14 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:short answer
Explore 7 Videos
Similar Questions
Knowledge Check
Out of the following which one is not a possible energy for a photon to be emitted by hydrogen atom according to Bohr's atomic model?
A0.65eVB1.9eVC11.1eVD13.6eV(A) bohr's third postulaate states that the stationary orbits are those for which the angular momentum is some integral multiple of h2π.
(R) linear momentum of the electron in the atom is quantised.Aif both assertion and reason are true and reason is the correct explanation of assertion.Bif both assertion and reason are true but reason is not the correct explanation of assertion.Cif assertion is true but reason is false.Dif both assertion and reason are false.
The angular momentum of an electron in the hydrogen atom is 3h2π Here. h is Planck's constant. The kinetic energy of this electron is
View SolutionThe energy of an excited hydrogen atom is 0.38 eV. Its angular momentum is n.h2π . Find n
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
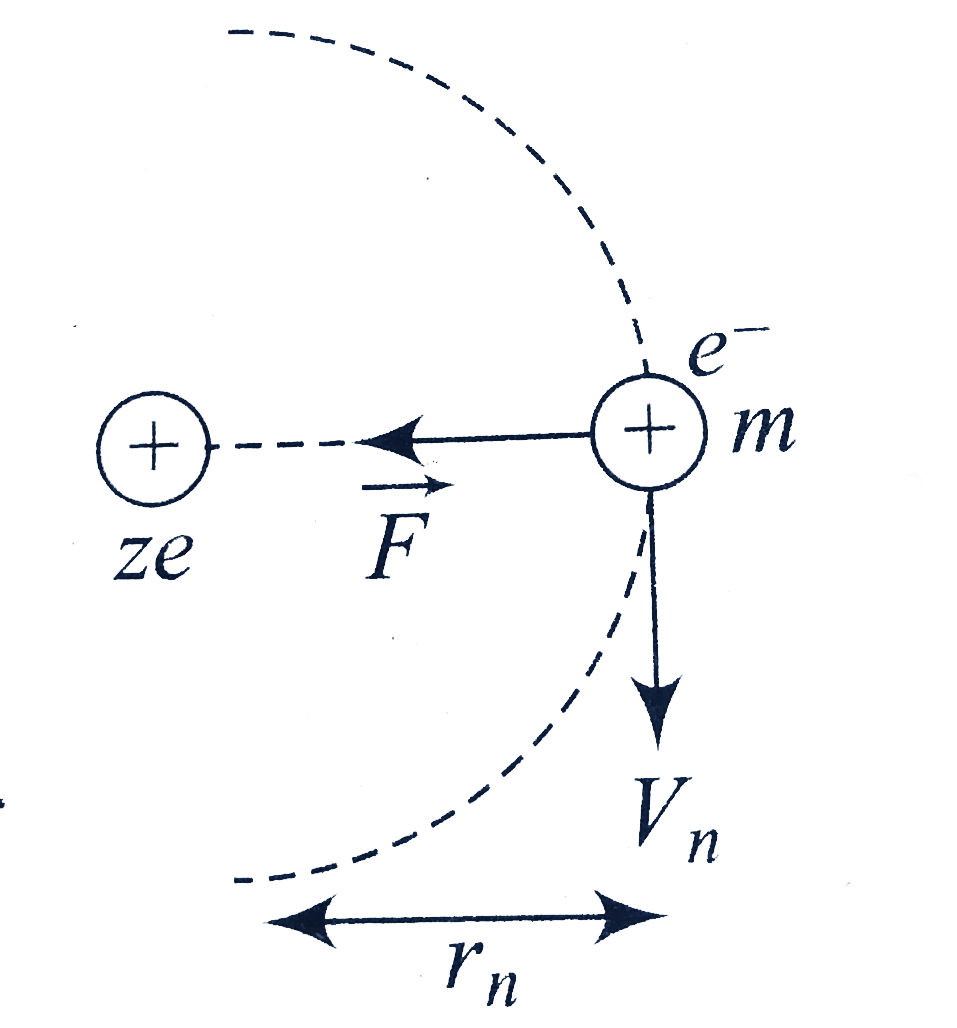
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planet, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multiple of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is 13.6eV. On the other planet, this ionization potential energy will be
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
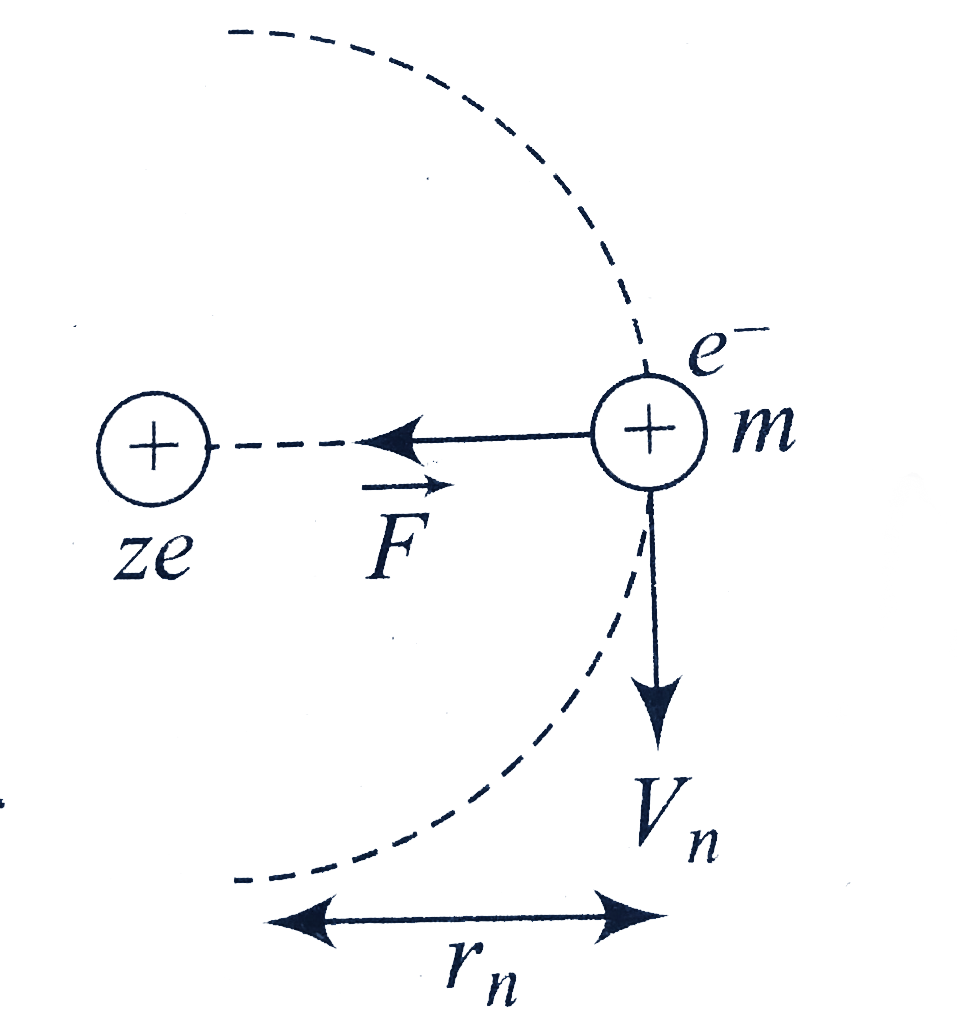
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should be
View SolutionSuppose in certine condition only those transition are allowed to hydrogen atoms in which the principal quantum number a changes by2 (a) Find the smaller wavelength emitted by hydrogen (b) list the wavelength emitted by hydrogen in the visible range (380nm→780nm)
View SolutionSuppose in certine condition only those transition are allowed to hydrogen atoms in which the principal quantum number a changes by2 (a) Find the smaller wavelength emitted by hydrogen (b) list the wavelength emitted by hydrogen in the visible range (380nm→780nm)
View Solution
