A hydrogen atom in state n=6 makes two successive transition and reaches the ground state in the first transition a photon of 1.13eV is emitted (a) Find the energy of the photon emitted in the second transition (b) what is the value of n in the intermediate state?
The correct Answer is:A, B, C
To solve the problem step by step, we will break it down into parts (a) and (b) as per the question.
1. Identify the initial and final states:
- The hydrogen atom starts in the state n=6 and transitions to the ground state n=1 through an intermediate state n=ni.
2. Calculate the energy of the initial state n=6:
- The energy of an electron in a hydrogen atom at a given principal quantum number n is given by:
En=−13.6eVn2
- For n=6:
E6=−13.6eV62=−13.6eV36≈−0.3778eV
3. Energy of the ground state n=1:
- For n=1:
E1=−13.6eV
4. Energy of the first transition:
- A photon of energy 1.13eV is emitted during the first transition from n=6 to n=ni.
- The energy difference can be expressed as:
E6−Eni=1.13eV
5. Calculate the energy of the intermediate state ni:
- Rearranging the equation gives:
Eni=E6−1.13eV
- Substituting E6:
Eni=−0.3778eV−1.13eV=−1.5078eV
6. Calculate the energy of the second transition:
- The energy emitted in the second transition is:
E2=E1−Eni
- Substituting the values:
E2=−13.6eV−(−1.5078eV)=−13.6+1.5078=−12.0922eV
- The energy of the photon emitted in the second transition is:
E2≈12.09eV
Part (b): Determine the value of n in the intermediate state.
1. Use the energy of the intermediate state:
- We already calculated the energy of the intermediate state Eni≈−1.5078eV.
2. Set up the equation for the intermediate state:
- Using the formula for energy:
Eni=−13.6eVn2i
- Setting this equal to the calculated energy:
−13.6n2i=−1.5078
3. Solve for n2i:
- Rearranging gives:
n2i=13.61.5078≈9.024
4. Calculate ni:
- Taking the square root:
ni≈3
Final Answers:
- (a) The energy of the photon emitted in the second transition is approximately 12.09 eV.
- (b) The value of n in the intermediate state is 3.
- The hydrogen atom starts in the state n=6 and transitions to the ground state n=1 through an intermediate state n=ni.
- The energy of an electron in a hydrogen atom at a given principal quantum number n is given by:
En=−13.6eVn2
- For n=6:
E6=−13.6eV62=−13.6eV36≈−0.3778eV
- For n=1:
E1=−13.6eV
- A photon of energy 1.13eV is emitted during the first transition from n=6 to n=ni.
- The energy difference can be expressed as:
E6−Eni=1.13eV
- Rearranging the equation gives:
Eni=E6−1.13eV
- Substituting E6:
Eni=−0.3778eV−1.13eV=−1.5078eV
- The energy emitted in the second transition is:
E2=E1−Eni
- Substituting the values:
E2=−13.6eV−(−1.5078eV)=−13.6+1.5078=−12.0922eV
- The energy of the photon emitted in the second transition is:
E2≈12.09eV
- We already calculated the energy of the intermediate state Eni≈−1.5078eV.
- Using the formula for energy:
Eni=−13.6eVn2i
- Setting this equal to the calculated energy:
−13.6n2i=−1.5078
- Rearranging gives:
n2i=13.61.5078≈9.024
- Taking the square root:
ni≈3
- (a) The energy of the photon emitted in the second transition is approximately 12.09 eV.
- (b) The value of n in the intermediate state is 3.
Topper's Solved these Questions
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Obejective - II
5 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Short answer
14 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
Similar Questions
The energy levels of a hypotherical one electron atom are shown in figure
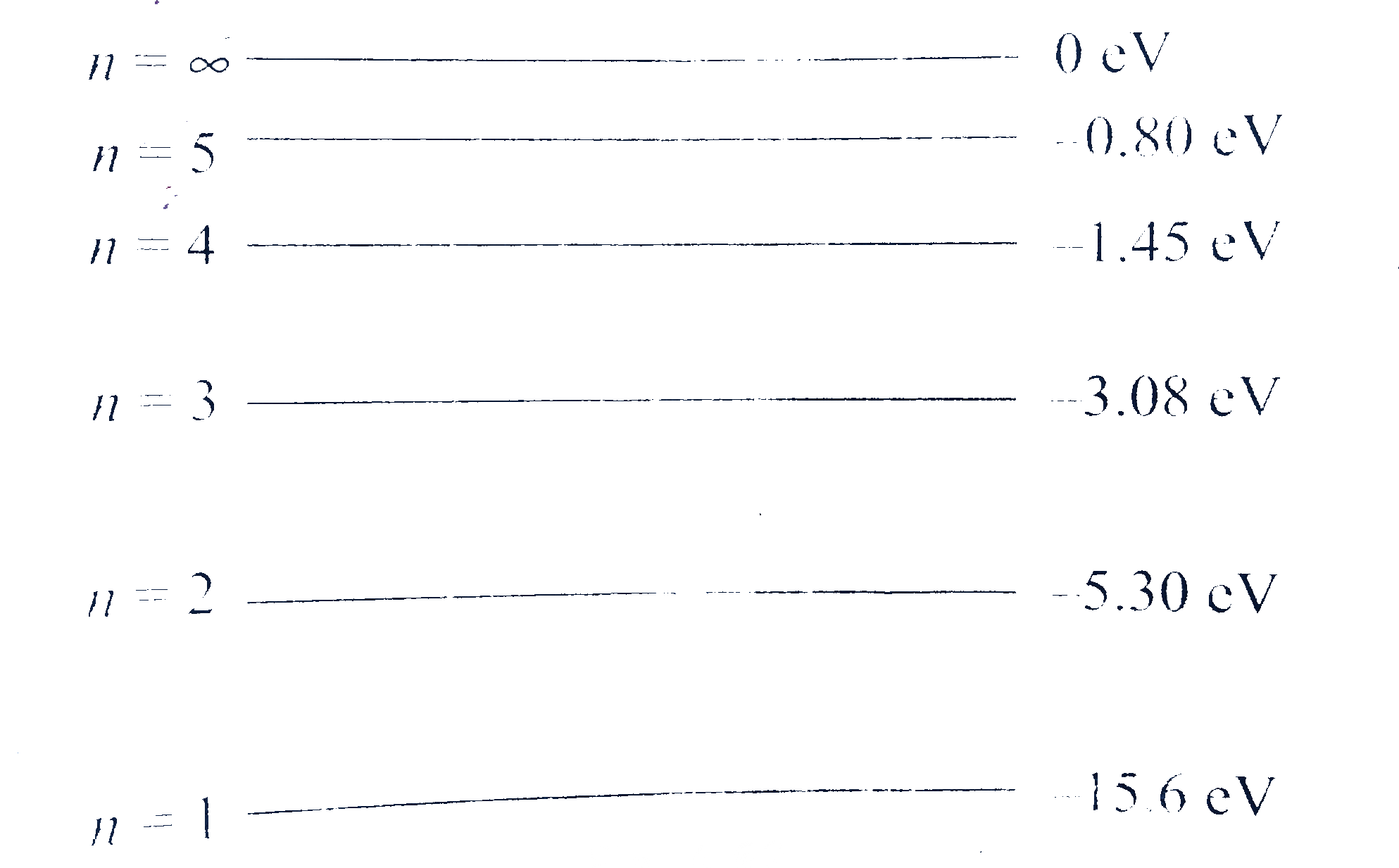
Find the wave number of the photon emitted for the transition n=3→n=1
View SolutionAs an electron makes a transition from an excited state to the ground state of a hydrogen - like atom /ion
View SolutionA hydrogen like atom in ground st6ate abserbs n photon having the same energy and its emit exacity n photon when electron transition tekes placed .Then the energy of the absorbed photon may be
View Solutionwhat are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n =2 state in the hydrogen atom?
View Solutionwhat are the frequency and wavelength of a photon emitted during a transition from n = 5 state to the n =2 state in the hydrogen atom?
View SolutionThe electron in a hydrogen atom makes a transition from an excited state to the ground state. Which of the following statements is true?
View SolutionThe electron in a hydrogen atom makes a transition from an excited state to the ground state. Which of the following statements is true?
View SolutionThe electron in a hydrogen atom at rest makes a transition from n=2 energy state to the n=1 ground state.
find the energy (eV) of the emitted photon.
View SolutionA hydrogen atom in a state of binding energy 0.85 eV makes a transition to a state of excitation energy of 10.2 eV . Find the energy and wavelength of photon emitted.
View SolutionA hydrogen atom in a state of binding energy 0.85 eV makes a transition to a state of excitation energy of 10.2 eV . Find the energy and wavelength of photon emitted.
View Solution

