Consider the situation of the previous problem. Find the average electric field energy stored in the capacitor and the average magnetic field energy stored in the coil.
Given R=300Ω, C=20μF
=20×10−6F, L=1H, Z=500(from 14) ,E0=50V, i0=E0Z=50500=0.1A
Electrical energy stored in capacitor
=12CV2
=12×20×10−5×50×50
=25×10−3J=25mJ.
Magnetic field energy stored in the coil
=12Li20
=12×1×(0.1)2
=12×1×10−2=5×10−3J
=5mJ
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Short answer14videos
ALTERNATING CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Objective 27videos
ALTERNATING CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
Similar Questions
(a) In a series L-C-R circuit with an AC source, R =300Ω, C = 20μF,L=1.0H,V0=50√2Vandf=50πHz. Find (i) the rms current in the circuit and (ii) the rms voltage across each element.
(b) Consider the situatiuon of the previous part. find the average electric field energy stored in the capacitor and the average magnetic field energy stored iun the coil .View SolutionThe energy stored in the capacitor in the steady state is
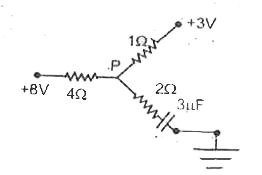
View SolutionIn the figure magnetic energy stored in the coil is
View SolutionThe energy stored in 4μF capacitors is
View SolutionIn a series LCR circuit with an ac source of 50V,R=300Ω,frequency v=50πHz.The average electric field energy, stored in the capacitor and average magnetic energy stored in the coil are 25mJ and 5mJ respectively.The RMS current in the circuit is 0.10A.Then find
View SolutionThe total electrostatic energy stored in both the capacitor is
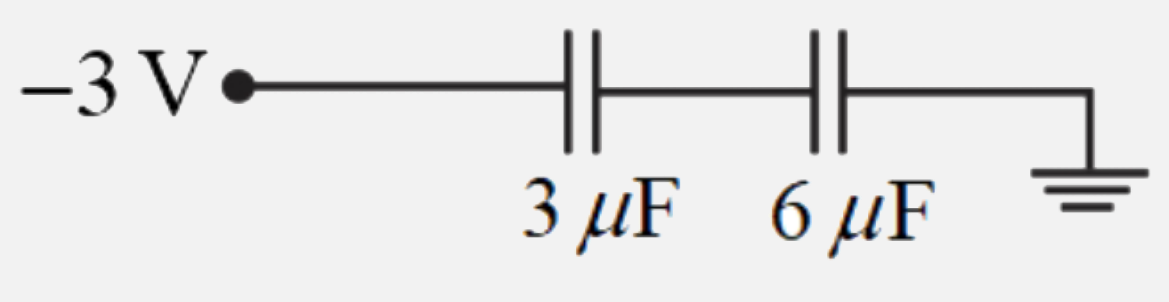
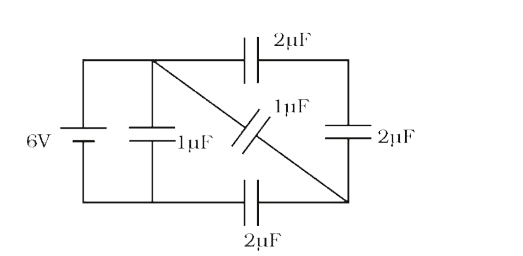
View SolutionFind the total energy stored in the capacitors in the given network.
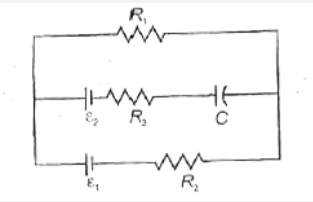
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
View SolutionMatch the columns
View SolutionFind the charge and energy stored on the capactor C in the electrical network shonw below .
View Solution
