Question

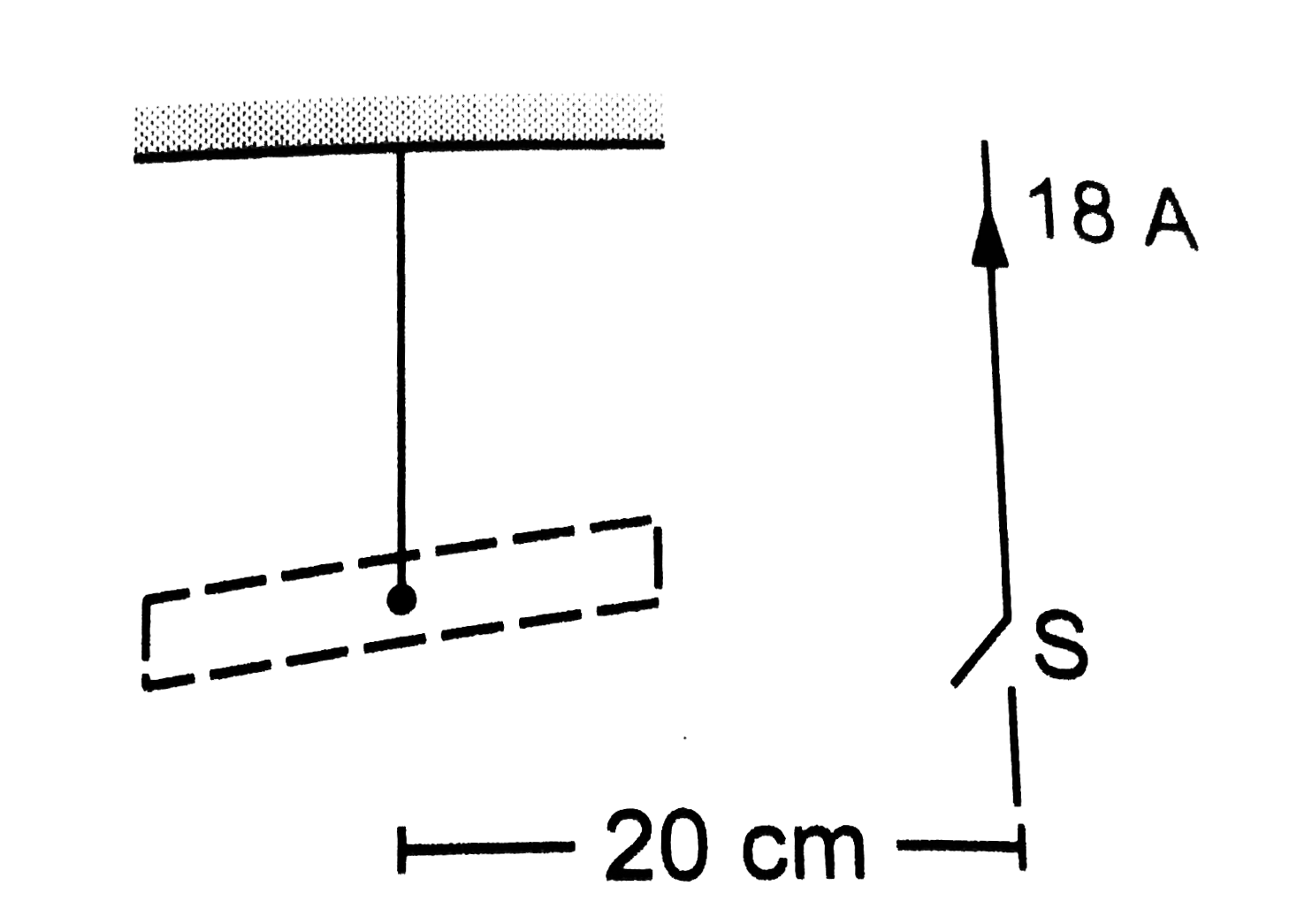
A short magnet oscillates in a vibration magnetometer with a time period of 0.10 s where the horizontal component of earth's magnetic field is $24\mu T$ . An upward current of 18 A is established in the vertical wire placed 20 cm east of the magnet . Find the new time period.

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the given information
- The initial time period \( T_1 \) of the magnet is \( 0.10 \, \text{s} \).
- The horizontal component of Earth's magnetic field \( B_H \) is \( 24 \, \mu T \) (microtesla).
- A vertical wire carrying a current of \( 18 \, A \) is placed \( 20 \, cm \) (or \( 0.2 \, m \)) east of the magnet.

Step 2: Calculate the magnetic field due to the current
The magnetic field \( B \) at a distance \( D \) from a long straight wire carrying a current \( I \) is given by the formula:
\( B = \frac{\mu_0 I}{2 \pi D} \)
Where:
- \( \mu_0 = 4 \pi \times 10^{-7} \, T \cdot m/A \) (permeability of free space)
- \( I = 18 \, A \)
- \( D = 0.2 \, m \)

Substituting the values:
\( B = \frac{(4 \pi \times 10^{-7}) \times 18}{2 \pi \times 0.2} \)
\( B = \frac{4 \times 10^{-7} \times 18}{0.4} \)
\( B = \frac{72 \times 10^{-7}}{0.4} = 180 \times 10^{-7} = 18 \, \mu T \)

Step 3: Determine the new effective magnetic field
When the current is flowing, the effective magnetic field \( B_{eff} \) acting on the magnet is the difference between the Earth's magnetic field and the magnetic field due to the current:
\( B_{eff} = B_H - B \)
Substituting the values:
\( B_{eff} = 24 \, \mu T - 18 \, \mu T = 6 \, \mu T \)

Step 4: Relate the time periods
The time period \( T \) of oscillation of a magnet in a magnetic field is given by:
\( T = 2 \pi \sqrt{\frac{I}{m B}} \)
Where \( I \) is the moment of inertia and \( m \) is the magnetic moment.

The ratio of the new time period \( T_2 \) to the original time period \( T_1 \) can be expressed as:
\( \frac{T_2}{T_1} = \sqrt{\frac{B_H}{B_{eff}}} \)
Substituting the values:
\( \frac{T_2}{T_1} = \sqrt{\frac{24 \, \mu T}{6 \, \mu T}} = \sqrt{4} = 2 \)

Step 5: Calculate the new time period
Now, we can find \( T_2 \):
\( T_2 = 2 \times T_1 = 2 \times 0.10 \, s = 0.20 \, s \)

Final Answer
The new time period \( T_2 \) is \( 0.20 \, s \).

---