A earth's magnetic field at geomagnetic poles has a magnitude 6.2×10−5T. Find the magnitude and the direction of the field at a point on the earth's surface where the radius makes an angle of 135∘ with the axis of the earth's assumed magnetic dipole. What is the inclination (dip) at this point?
To solve the problem, we need to find the magnitude and direction of the Earth's magnetic field at a point where the radius makes an angle of 135∘ with the axis of the Earth's assumed magnetic dipole. Additionally, we need to determine the inclination (dip) at this point.
1. Understanding the Magnetic Field at the Geomagnetic Poles:
The Earth's magnetic field at the geomagnetic poles is given as:
Bpole=6.2×10−5T
2. Magnetic Field on the Axis of a Dipole:
The magnetic field B on the axis of a magnetic dipole is given by:
B=μ04π⋅2mr3
where m is the magnetic moment, r is the distance from the dipole, and μ0 is the permeability of free space.
3. Relating the Given Magnetic Field to the Dipole Moment:
At the poles, the magnetic field can be expressed as:
Bpole=μ04π⋅2mr3=6.2×10−5T
From this, we can derive:
μ04π⋅2mr3=6.2×10−5⟹μ04π⋅mr3=3.1×10−5
4. Magnetic Field at an Angle:
The magnetic field at a general point on the Earth's surface, where the radius makes an angle θ with the axis, is given by:
B=μ04π⋅mr3√1+3cos2θ
Here, θ=135∘.
5. Calculating cos(135∘):
cos(135∘)=−1√2(or approximately -0.707)
Therefore,
cos2(135∘)=(−1√2)2=12
6. Substituting Values:
Now substituting back into the equation for B:
B=3.1×10−5√1+3⋅12=3.1×10−5√1+1.5=3.1×10−5√2.5
B≈3.1×10−5×1.58≈4.9×10−5T
7. Finding the Inclination (Dip):
The angle of dip ϕ is related to the angle θ by:
tanα=tanθ2
Here, θ=135∘, so:
tan(135∘)=−1⟹tanα=−12⟹α=tan−1(−0.5)
This gives:
α≈−26.57∘
The angle of dip ϕ is then:
ϕ=α−90∘≈−26.57∘−90∘≈−116.57∘
Final Answers
- Magnitude of the Magnetic Field: 4.9×10−5T
- Inclination (Dip): 63∘ (since we consider the absolute value)
The Earth's magnetic field at the geomagnetic poles is given as:
Bpole=6.2×10−5T
The magnetic field B on the axis of a magnetic dipole is given by:
B=μ04π⋅2mr3
where m is the magnetic moment, r is the distance from the dipole, and μ0 is the permeability of free space.
At the poles, the magnetic field can be expressed as:
Bpole=μ04π⋅2mr3=6.2×10−5T
From this, we can derive:
μ04π⋅2mr3=6.2×10−5⟹μ04π⋅mr3=3.1×10−5
The magnetic field at a general point on the Earth's surface, where the radius makes an angle θ with the axis, is given by:
B=μ04π⋅mr3√1+3cos2θ
Here, θ=135∘.
cos(135∘)=−1√2(or approximately -0.707)
Therefore,
cos2(135∘)=(−1√2)2=12
Now substituting back into the equation for B:
B=3.1×10−5√1+3⋅12=3.1×10−5√1+1.5=3.1×10−5√2.5
B≈3.1×10−5×1.58≈4.9×10−5T
The angle of dip ϕ is related to the angle θ by:
tanα=tanθ2
Here, θ=135∘, so:
tan(135∘)=−1⟹tanα=−12⟹α=tan−1(−0.5)
This gives:
α≈−26.57∘
The angle of dip ϕ is then:
ϕ=α−90∘≈−26.57∘−90∘≈−116.57∘
- Magnitude of the Magnetic Field: 4.9×10−5T
- Inclination (Dip): 63∘ (since we consider the absolute value)
Topper's Solved these Questions
- PERMANENT MAGNETSBook:HC VERMA ENGLISHChapter:PERMANENT MAGNETSExercise:Objective
Explore 13 Videos
- PERMANENT MAGNETSBook:HC VERMA ENGLISHChapter:PERMANENT MAGNETSExercise:Objective II
Explore 1 Video
- PERMANENT MAGNETSBook:HC VERMA ENGLISHChapter:PERMANENT MAGNETSExercise:Short Answer
Explore 11 Videos
- OPTICAL INSTRUMENTSBook:HC VERMA ENGLISHChapter:OPTICAL INSTRUMENTSExercise:Question for short Answer
Explore 12 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:question for short answer
Explore 13 Videos
Similar Questions
The earth's magnetic field at geomagnetic poles has a magnitude 8×10−5T. Find the magnitude and the direction of the field at a point on the earth's surface where the radius makes an angle of 120∘ with its axis of the earth's assumed magnetic dipole. What is the inclination dip at this point?
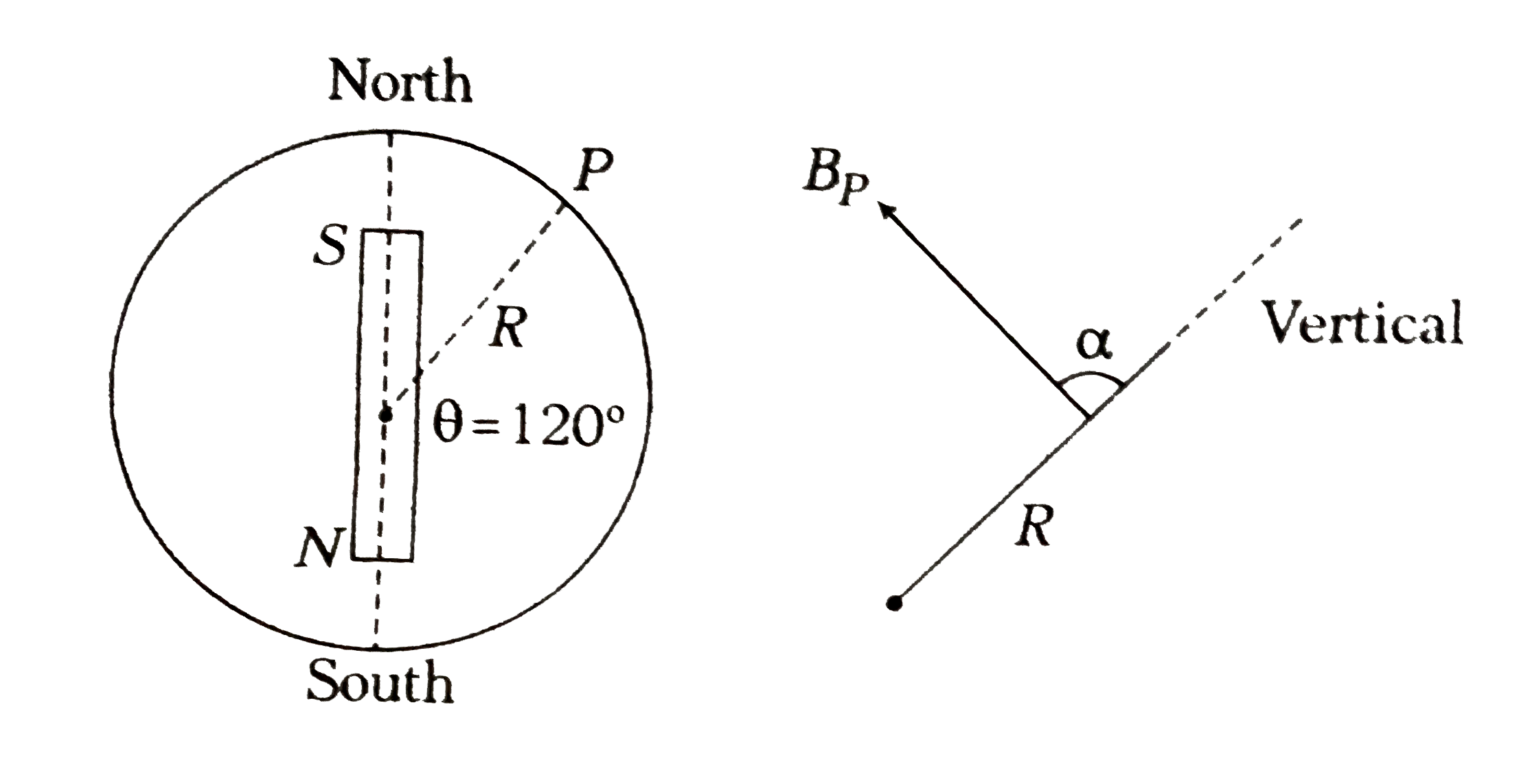
View SolutionFind the magnitude and direction of magnetic field at point O in the following case

View Solution
Knowledge Check
The magnetic field of Earth can be modelled by that of a point dipole placed at the centre of the Earth. The dipole axis makes an angle of 11⋅3∘ with the axis of Earth. At Mumbai, declination is nearly zero. Then,
Athe declination varies between 11.3∘Wto11.3∘WBthe least declination is 0∘Cthe plane defined by dipole axis and the earth axis passes through Greenwich.Ddeclination averaged over the earth must be always negative.
Evaluate magnitude and direction of magnetic field at a point P in the following cases
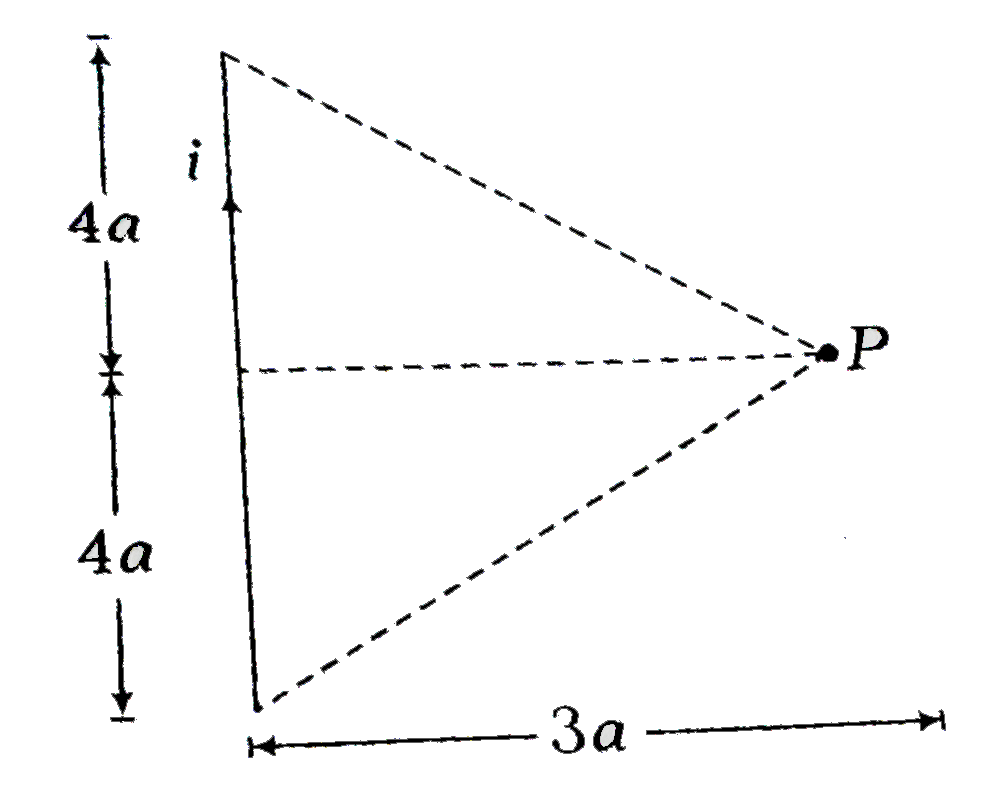

View SolutionIf the earth's magnetic field has a magnitude 3.4×10−5T at the magnetic equator of the earth, what would be its value at the earth's goemagnetic poles?
View SolutionThe magnitude of earth magnetic field at magnetic equator is 2.8×10−5T . Find magnitude of earth's magnetic field near geomagnetic poles .
View SolutionThe magnetic field of the earth can be modelled by that of a point dipole placed at the centre of the earth. The dipole axis makes an angle of 11.3∘ with the axis of the earth. At mumbai, declination is nearlyzero, then.
View SolutionThe horizontal component of the earth's magnetic field is 3.6×10−5T where the dip is 60∘. Find the magnitude of the earth's magnetic field.
View SolutionShow that the magnetic field at a point due to a magnetic dipole is perpendicular to the magnetic axis if the line joining the point with the centre of the dipole makes an angle of tan−1(√2) with the magnetic axis.
View SolutionLet the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator
View Solution