A proton is projected with a speed of 3X106ms−1 horizontally from est to west. A uniform magnetic field →Bofstren>h2.0X10−3 T exists in the vertically upward direction(a) find the force on the proton just after it is projected. (b) what is the acceleration produced?
To solve the problem step by step, we will break it down into two parts: (a) finding the force on the proton and (b) finding the acceleration produced.
Part (a): Finding the Force on the Proton
1. Identify the given values:
- Speed of the proton, v=3×106m/s
- Magnetic field strength, B=2×10−3T
- Charge of the proton, q=1.6×10−19C
2. Use the formula for magnetic force:
The magnetic force F on a charged particle moving in a magnetic field is given by:
F=qvBsin(θ)
where θ is the angle between the velocity vector and the magnetic field vector. In this case, since the proton is moving horizontally and the magnetic field is vertical, θ=90∘.
3. Calculate sin(90∘):
sin(90∘)=1
4. Substitute the values into the formula:
F=(1.6×10−19C)×(3×106m/s)×(2×10−3T)×1
5. Perform the calculation:
F=1.6×3×2×10−19×106×10−3
F=9.6×10−16N
Part (b): Finding the Acceleration Produced
1. Use the formula for acceleration:
The acceleration a can be calculated using Newton's second law:
a=Fm
where m is the mass of the proton.
2. Identify the mass of the proton:
The mass of the proton is approximately:
m=1.67×10−27kg
3. Substitute the values into the formula:
a=9.6×10−16N1.67×10−27kg
4. Perform the calculation:
a=5.74×1011m/s2
Final Answers:
- (a) The force on the proton is 9.6×10−16N.
- (b) The acceleration produced is 5.74×1011m/s2.
- Speed of the proton, v=3×106m/s
- Magnetic field strength, B=2×10−3T
- Charge of the proton, q=1.6×10−19C
The magnetic force F on a charged particle moving in a magnetic field is given by:
F=qvBsin(θ)
where θ is the angle between the velocity vector and the magnetic field vector. In this case, since the proton is moving horizontally and the magnetic field is vertical, θ=90∘.
sin(90∘)=1
F=(1.6×10−19C)×(3×106m/s)×(2×10−3T)×1
F=1.6×3×2×10−19×106×10−3
F=9.6×10−16N
The acceleration a can be calculated using Newton's second law:
a=Fm
where m is the mass of the proton.
The mass of the proton is approximately:
m=1.67×10−27kg
a=9.6×10−16N1.67×10−27kg
a=5.74×1011m/s2
- (a) The force on the proton is 9.6×10−16N.
- (b) The acceleration produced is 5.74×1011m/s2.
Topper's Solved these Questions
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:worked out Examples
Explore 11 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective 1
Explore 10 Videos
- LIGHT WAVESBook:HC VERMA ENGLISHChapter:LIGHT WAVESExercise:Question for short Answer
Explore 11 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
Similar Questions
A proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionAn electron is projectd horizontally with a kinetic energy of 10 keV. A magnetic feld of strength 1.0X10−7 T exists in the vertically upward direction. (a)will the electron deflect towards right or towards left of its motion? (b) calculate the sideways deflection of the electrion in travelling through 1m. make appropriate approximations.
View SolutionA charge of2.0μC moves with a speed of 2.0X106ms−1 along the positive x-axis. A magnetic field →B of strength (0.20→J+0.40→k)T exists in space. Find the magnetic force acting on the charge
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionA particle having a charge of 2.0X10−8C and a mass of 2.0X10−10g is projected with a speed of 2.0X103ms−1 in a region having a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
View SolutionTwo protons are projected simultaneously from a fixed point with the same velocity v into a region, magnetic there exists a uniform magnetic field. The magnetic field strength at B and it si perpendicular to the initial direction of v. One proton starts at time t=0 and another proton at t=πm2qB. The separation between them at time t=πmqB (where, m and q are the mass and charge of proton), will be approximately
View SolutionA body is projected horizontally from a height of 78.4 m with a velocity 10 ms−1 . Its velocity after 3 seconds is [g = 10 ms−2] (Take direction of projection on →i and vertically upward direction on j)
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.
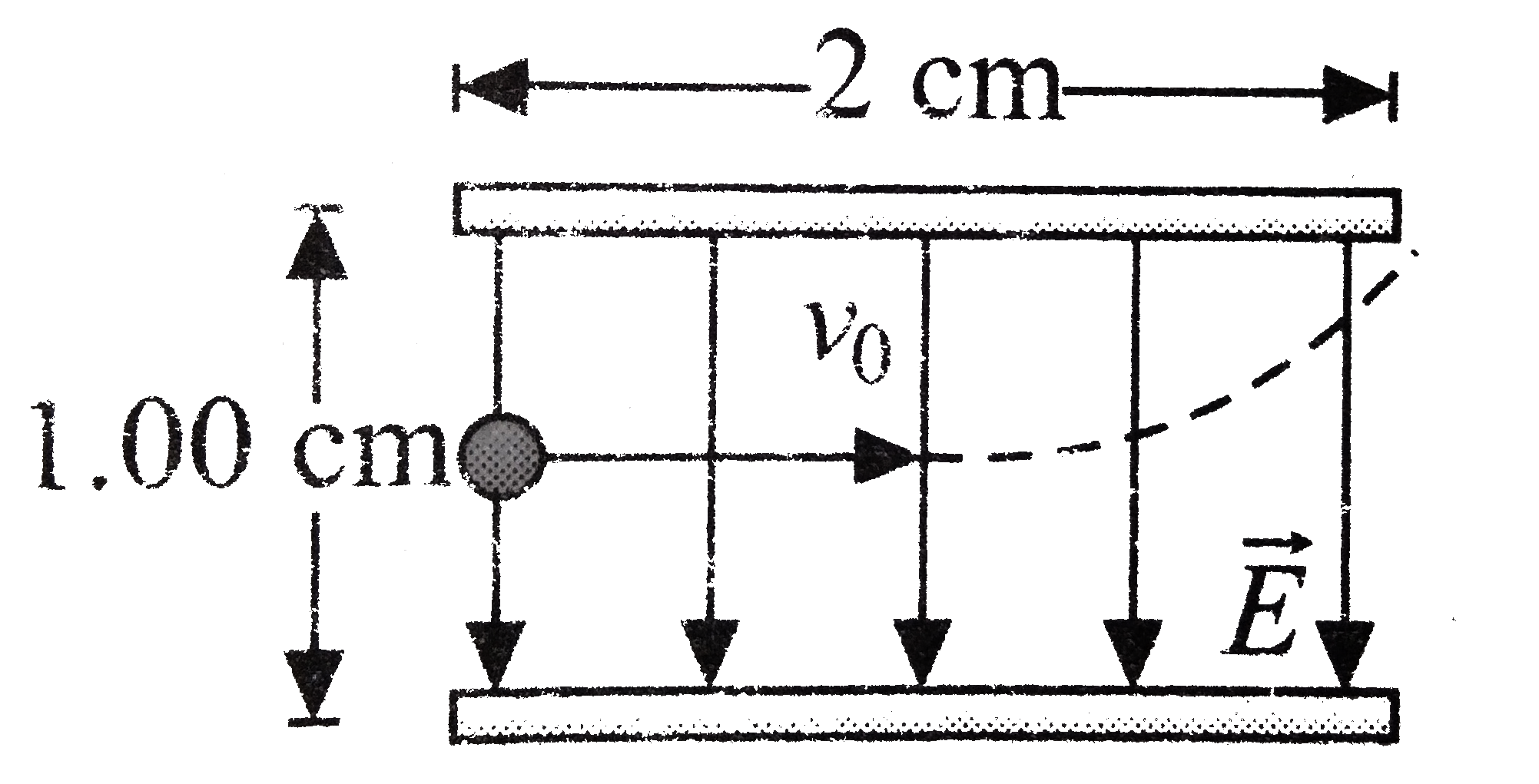
The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionAn electron is projected with an initial speed v0=1.60×106ms−1 into the uniform field between the parallel plates as shown in fig. Assume that the field between the plates is uniform and directed vertically downward, and that the field outside the plates is zero. the electrons enters the field at a point midway between the plates. Mass of electron is 9.1×10−31kg.

The vertical displacement traveled by the proton as it exits the region between the plated is (mass pf proton is 1.67×10−27kg).
View SolutionA proton (charge 1.6×10−19C,mass=1.67×10−27kg) is shot with a speed 8×106ms−1 at an angle of 30∘ with the X-axis. A uniform magnetic field B=0.30T exists along the X-axis. Show that path of the proton is a helix. Find the radius and pitch of the helix.
View Solution
