Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0×105Nm−2 from the following data. Density of kerosene =800kgm−3 and speed of sound in kerosene =1330ms−1
The correct Answer is:A, C, D
To find the change in volume of 1.0 liter of kerosene when subjected to an extra pressure of 2.0×105N/m2, we can follow these steps:
Step 1: Convert Volume to Cubic Meters
1. The volume of kerosene is given as 1.0 liter.
2. Convert liters to cubic meters:
V=1.0liters=1.0×10−3m3
Step 2: Identify Given Values
1. The extra pressure (ΔP) is given as:
ΔP=2.0×105N/m2
2. The density (ρ) of kerosene is:
ρ=800kg/m3
3. The speed of sound in kerosene (v) is:
v=1330m/s
Step 3: Calculate Bulk Modulus
1. The bulk modulus (K) can be calculated using the formula:
K=ρv2
2. Substitute the values:
K=800kg/m3×(1330m/s)2
Step 4: Calculate Change in Volume
1. The change in volume (ΔV) can be calculated using the formula derived from the bulk modulus:
ΔV=VΔPK
2. Substitute the values:
ΔV=1.0×10−3m3×2.0×105N/m2K
Step 5: Perform the Calculations
1. Calculate K:
K=800×(1330)2=800×1768900=1415120000N/m2
2. Now substitute K back into the change in volume equation:
ΔV=1.0×10−3×2.0×1051415120000
3. Calculate ΔV:
ΔV=2.0×10−31415120000≈0.14×10−6m3
Step 6: Convert to Centimeter Cubes
1. Convert ΔV from cubic meters to cubic centimeters:
ΔV≈0.14cm3
Final Answer
The change in volume of 1.0 liter of kerosene when subjected to an extra pressure of 2.0×105N/m2 is approximately 0.14cm3.
---
1. The volume of kerosene is given as 1.0 liter.
2. Convert liters to cubic meters:
V=1.0liters=1.0×10−3m3
1. The extra pressure (ΔP) is given as:
ΔP=2.0×105N/m2
2. The density (ρ) of kerosene is:
ρ=800kg/m3
3. The speed of sound in kerosene (v) is:
v=1330m/s
1. The bulk modulus (K) can be calculated using the formula:
K=ρv2
2. Substitute the values:
K=800kg/m3×(1330m/s)2
1. The change in volume (ΔV) can be calculated using the formula derived from the bulk modulus:
ΔV=VΔPK
2. Substitute the values:
ΔV=1.0×10−3m3×2.0×105N/m2K
1. Calculate K:
K=800×(1330)2=800×1768900=1415120000N/m2
2. Now substitute K back into the change in volume equation:
ΔV=1.0×10−3×2.0×1051415120000
3. Calculate ΔV:
ΔV=2.0×10−31415120000≈0.14×10−6m3
1. Convert ΔV from cubic meters to cubic centimeters:
ΔV≈0.14cm3
The change in volume of 1.0 liter of kerosene when subjected to an extra pressure of 2.0×105N/m2 is approximately 0.14cm3.
Topper's Solved these Questions
Similar Questions
The rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
View SolutionThe rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
View SolutionThe bulk modulus of mercury is 2.8×1010 N/m2 and the density is 13600 kg/m2. What is the speed of sound in mercury ?
View Solution_E01_206_Q01.png)
The container shown below holds kerosene and air as indicated compute the pressure at P,Q,R and S in KN/m2 take spacific gravity of kerosene as 0.8
View SolutionFind the decrease in the volume of a simple of water from the following data. Initial volume =2000cm−2 , initial pressure =105Nm−2 , final pressure =106N−1m2.
View SolutionFind the greatest length of steel wire that can hang vertically without breaking. Breaking stress of steel =8.0×108N/m2. Density of steel =8.0×103kg/m3. Take g=10m/s2.
View SolutionCalculate the speed of efflux of kerosene oil from an orifice of a tank in which pressure is 4 atmosphere. Density of kerosene oil = 0.72 kg /lite.
View SolutionFor a person with normal hearing, the faintest sound that can be at a frequency of 400Hz has pressure amplitude of about 6.0×10−5 Pa . Calculate the corresponding intensity in W/m2 . Take speed of sound in air as 344m/s and density of air 1.2kg/m3 .
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
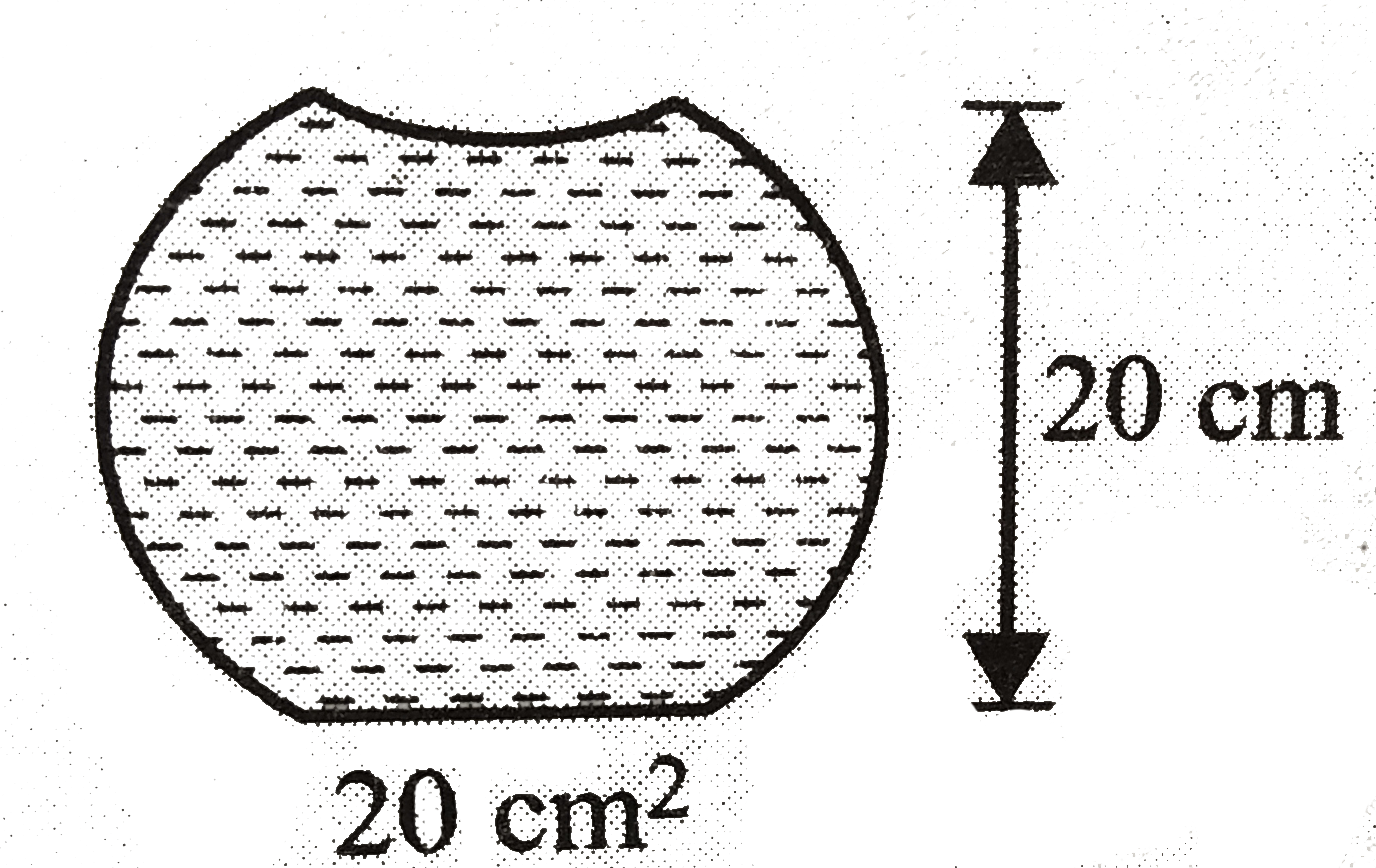
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionIf the density of wood is 800kg/m3 and volume is 0.3m3 find its mass.
View Solution
