Find the dispersive power of flint glass. The refractive indices of flint glass for red, yellow and violet light are 1.613, 1.620 and 1.632 respectively.
To find the dispersive power of flint glass, we can follow these steps:
Step 1: Understand the formula for dispersive power
The dispersive power (ω) is given by the formula:
ω=μv−μrμy−1
where:
- μv = refractive index for violet light
- μr = refractive index for red light
- μy = refractive index for yellow light
Step 2: Identify the given values
From the question, we have the following refractive indices:
- μr=1.613 (for red light)
- μy=1.620 (for yellow light)
- μv=1.632 (for violet light)
Step 3: Substitute the values into the formula
Now, we substitute the values into the dispersive power formula:
ω=1.632−1.6131.620−1
Step 4: Calculate the numerator
Calculate the difference in the numerator:
1.632−1.613=0.019
Step 5: Calculate the denominator
Calculate the difference in the denominator:
1.620−1=0.620
Step 6: Divide the results
Now, we can divide the results from the numerator and denominator:
ω=0.0190.620
Step 7: Perform the division
Calculating the division gives:
ω≈0.030645
Step 8: Round the answer
Rounding to three decimal places, we find:
ω≈0.031
Conclusion
Thus, the dispersive power of flint glass is approximately 0.031.
---
The dispersive power (ω) is given by the formula:
ω=μv−μrμy−1
where:
- μv = refractive index for violet light
- μr = refractive index for red light
- μy = refractive index for yellow light
From the question, we have the following refractive indices:
- μr=1.613 (for red light)
- μy=1.620 (for yellow light)
- μv=1.632 (for violet light)
Now, we substitute the values into the dispersive power formula:
ω=1.632−1.6131.620−1
Calculate the difference in the numerator:
1.632−1.613=0.019
Calculate the difference in the denominator:
1.620−1=0.620
Now, we can divide the results from the numerator and denominator:
ω=0.0190.620
Calculating the division gives:
ω≈0.030645
Rounding to three decimal places, we find:
ω≈0.031
Thus, the dispersive power of flint glass is approximately 0.031.
Topper's Solved these Questions
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Worked out Examples
Explore 3 Videos
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Objective -1
Explore 5 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:short answer
Explore 7 Videos
- ELECTRIC CURRENT IN CONDUCTORSBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT IN CONDUCTORSExercise:questions for short answer
Explore 17 Videos
Similar Questions
The refractive indicates of flint glass for red and violent colours are 1.644and1.664. Calculate its dispersive power.
View SolutionWe have to combine a crown glass prism of angle 4∘ with a flint glass prism in such a way that the mean ray passes undeviated, find (i) the angle of the flint glass prism needed and (i) the angular dispersion produced by the combination when white light goes through it. Refractive indices for red, yellow and violet light are 1.514, 1.517 and 1.523 respectively for crown glass and 1.613, 1.620 and 1.632 for flint glass.
View SolutionA crown glass prism of angle 5∘ is to be combined with a flint glass prism in such a way that the mean ray passes undeviated. Find (a) the angle of the flint glass prism needed and (b) the angular dispersion produced by the combination when white light goes through it. Refractive indices for red, yellow and viloet light are 1.514, 1.517 and 1.523 respectively for crown glass and 1.613 1.620 and 1.632 for flint glass.
View SolutionA crown glass prism of angle 5∘ is to be combined with a flint prism in such a way that the mean ray passes undeviated. Find (a) the angle of the flint glass prism needed and (b) the angular dispersion produced by the combinatino when white light goes through it. Refractive indices for red, yellow, and violet light are 1.541, 1.517 and 1.523, repectively, for crown flass and 1.613, 1.620 and 1.632 for flint glass.
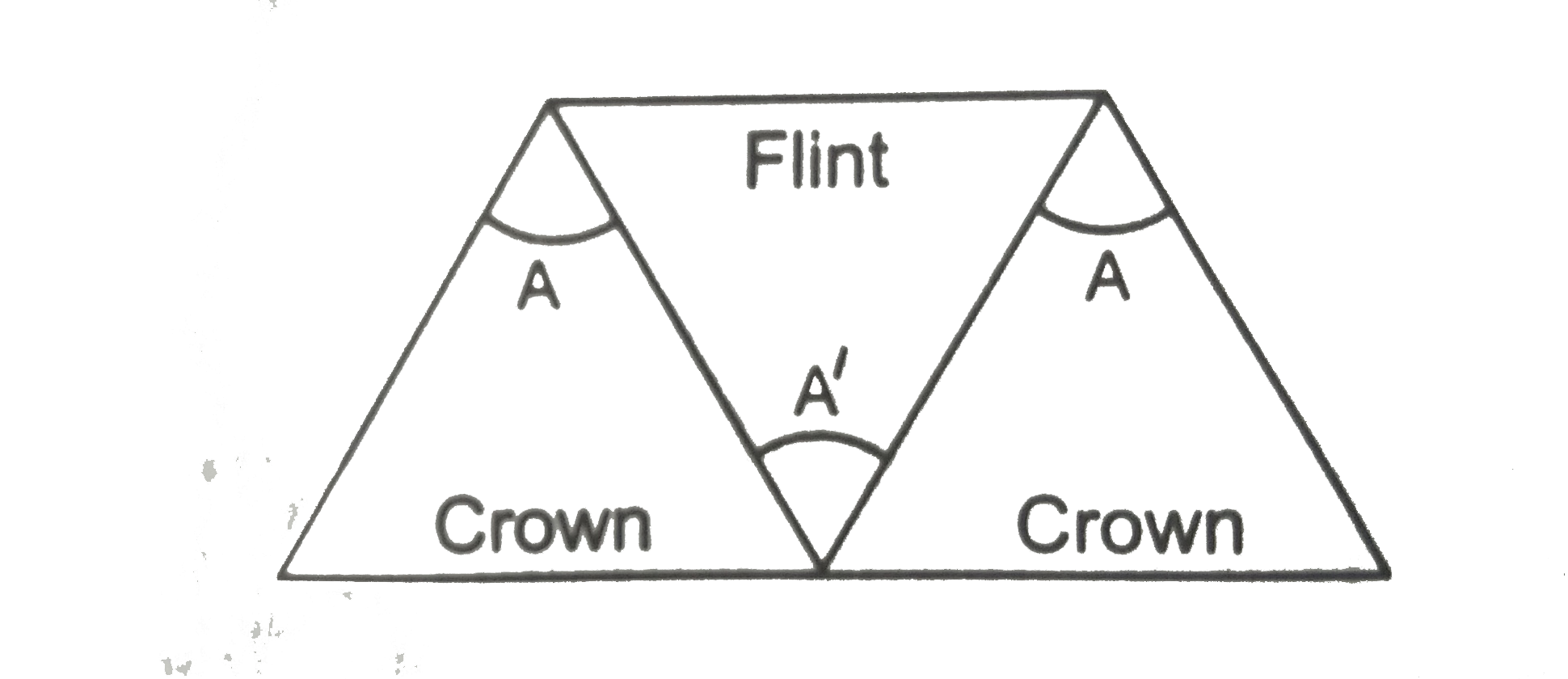
View SolutionThree thin prisms are combined as shown in figure. The refractive indices of the crown glass for red, yellow and violet rays are μr,μyandμv respectively and those for the flint glass are μ′r,μ′yandμ′v respectively. Find the ratio A'/A for which (a) there is no net angular dispersion, and (b) there is no net deviation in the yellow ray.
View SolutionThe refractive indices of flint glass for red and violet light are 1.613 and 1.632, respectively. Find the angular dispersion produced by the thin prism of flint glass having refracting angle 4∘.
View SolutionThe refractive indices of flint glass for red and violet lights are 1.613 and 1.632, respectively. Find the angular dispersion produced by a thin prism of flint glass having refracting angle 5∘.
View SolutionThe refractive indices of filnt glass for red and violet light are 1.613 and 1.632 respectively. Find the angular dispersion prouduced by a thin prism of flint glass having refracting angle 5∘
View SolutionA flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0∘, what would be the refracting angle of the crown prism ?
View SolutionThe refractive index of glass is 1.5. Find the speed of light in glass.
View Solution