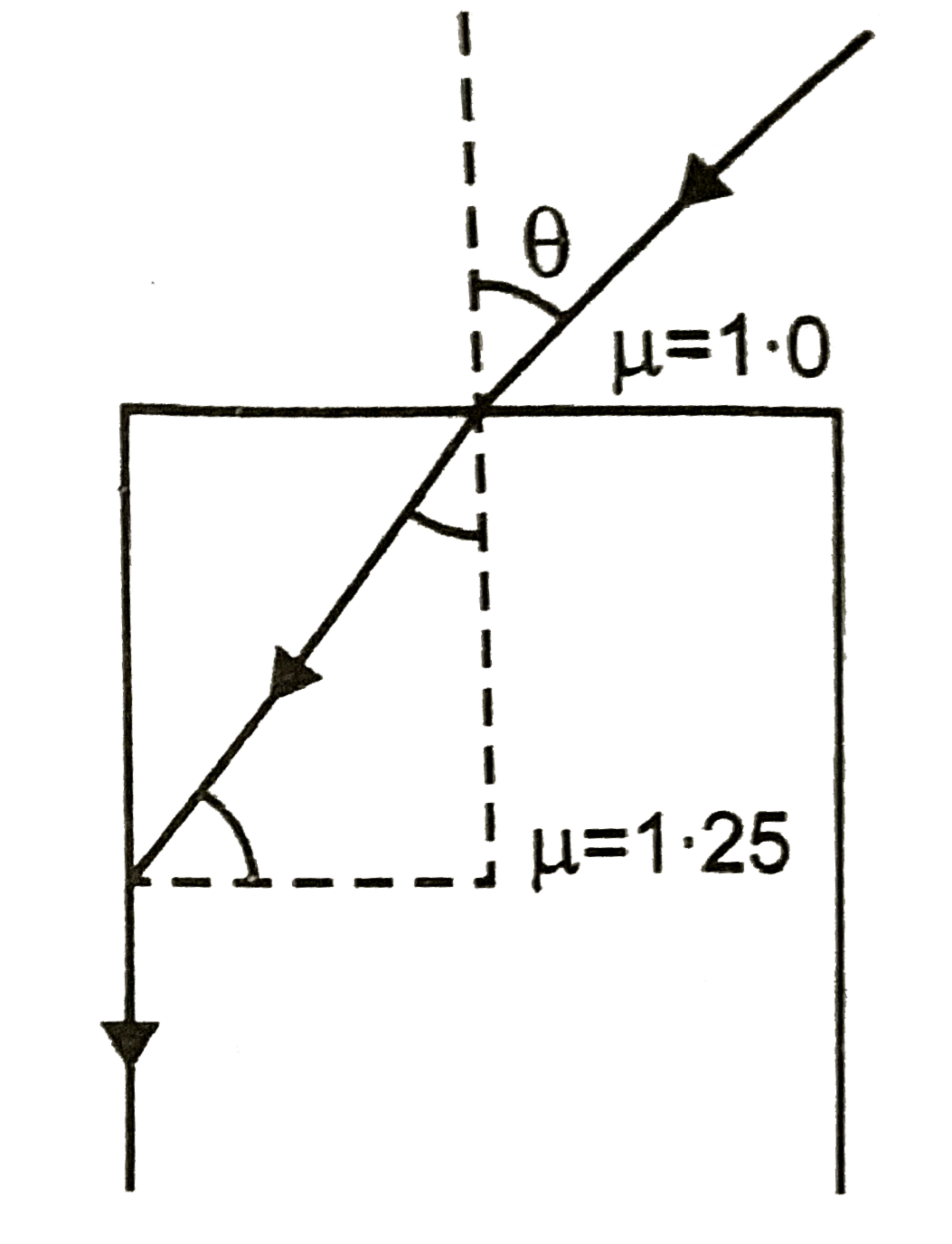
Consider the situation shown in figure. Find the maximum angle theta for which the light suffers total internal reflection at the vertical surface.
To solve the problem of finding the maximum angle θ for which light suffers total internal reflection at the vertical surface, we will follow these steps:
1. Understand Total Internal Reflection:
Total internal reflection occurs when light travels from a medium with a higher refractive index to a medium with a lower refractive index. The critical angle C is the angle of incidence above which total internal reflection occurs.
2. Calculate the Critical Angle:
The critical angle C can be calculated using the formula:
sinC=1μ
where μ is the refractive index of the medium from which light is coming. Given μ=1.25:
sinC=11.25=45
3. Determine the Angle θ1:
Since sinC=45, we can find θ1 (the angle of incidence at the vertical surface) using:
θ1=sin−1(45)
4. Construct a Right Triangle:
To visualize the situation, we can construct a right triangle where:
- The opposite side (perpendicular) is 4,
- The hypotenuse is 5.
Using the Pythagorean theorem, we can find the adjacent side (base):
Base=√52−42=√25−16=√9=3
5. Calculate θ2:
Since θ1+θ2=90∘, we have:
θ2=90∘−θ1
Using the sine and cosine relationship:
sinθ2=cosθ1
From our triangle, we have:
cosθ1=BaseHypotenuse=35
6. Apply Snell's Law:
According to Snell's law:
sinθsinθ2=μ
Substituting sinθ2=cosθ1=35:
sinθ=μ⋅sinθ2=1.25⋅35=34
7. Find the Angle θ:
Finally, we find θ:
θ=sin−1(34)
Final Result:
The maximum angle θ for which light suffers total internal reflection at the vertical surface is:
θ=sin−1(34)
Total internal reflection occurs when light travels from a medium with a higher refractive index to a medium with a lower refractive index. The critical angle C is the angle of incidence above which total internal reflection occurs.
The critical angle C can be calculated using the formula:
sinC=1μ
where μ is the refractive index of the medium from which light is coming. Given μ=1.25:
sinC=11.25=45
Since sinC=45, we can find θ1 (the angle of incidence at the vertical surface) using:
θ1=sin−1(45)
To visualize the situation, we can construct a right triangle where:
- The opposite side (perpendicular) is 4,
- The hypotenuse is 5.
Using the Pythagorean theorem, we can find the adjacent side (base):
Base=√52−42=√25−16=√9=3
Since θ1+θ2=90∘, we have:
θ2=90∘−θ1
Using the sine and cosine relationship:
sinθ2=cosθ1
From our triangle, we have:
cosθ1=BaseHypotenuse=35
According to Snell's law:
sinθsinθ2=μ
Substituting sinθ2=cosθ1=35:
sinθ=μ⋅sinθ2=1.25⋅35=34
Finally, we find θ:
θ=sin−1(34)
The maximum angle θ for which light suffers total internal reflection at the vertical surface is:
θ=sin−1(34)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Objective -1
Explore 15 Videos
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Objective -2
Explore 7 Videos
- GAUSS LAWBook:HC VERMA ENGLISHChapter:GAUSS LAWExercise:Short Question
Explore 7 Videos
- LIGHT WAVESBook:HC VERMA ENGLISHChapter:LIGHT WAVESExercise:Question for short Answer
Explore 11 Videos
Similar Questions
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is.
 .
.
View SolutionFor a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.

View SolutionConsider the situation shown in the figure.
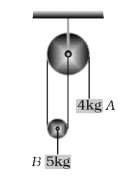
Find acceleration of A.
View SolutionConsider the situation shown in the figure.
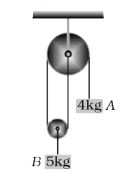
Find acceleration of B.
View SolutionWhich of the following is not due to total internal reflection ?
View SolutionA long solid cylindrical glass rod of refractive index 3/2 is immersed in a liquid of refractive index 3√34. The ends of the rod are perpendicular to the central axis of the rod. A light enters one end of the rod at the central axis as shown in the figure . find the maximum value of angle θ for which total internal reflection occurs inside the rod?
_E01_131_Q01.png)
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
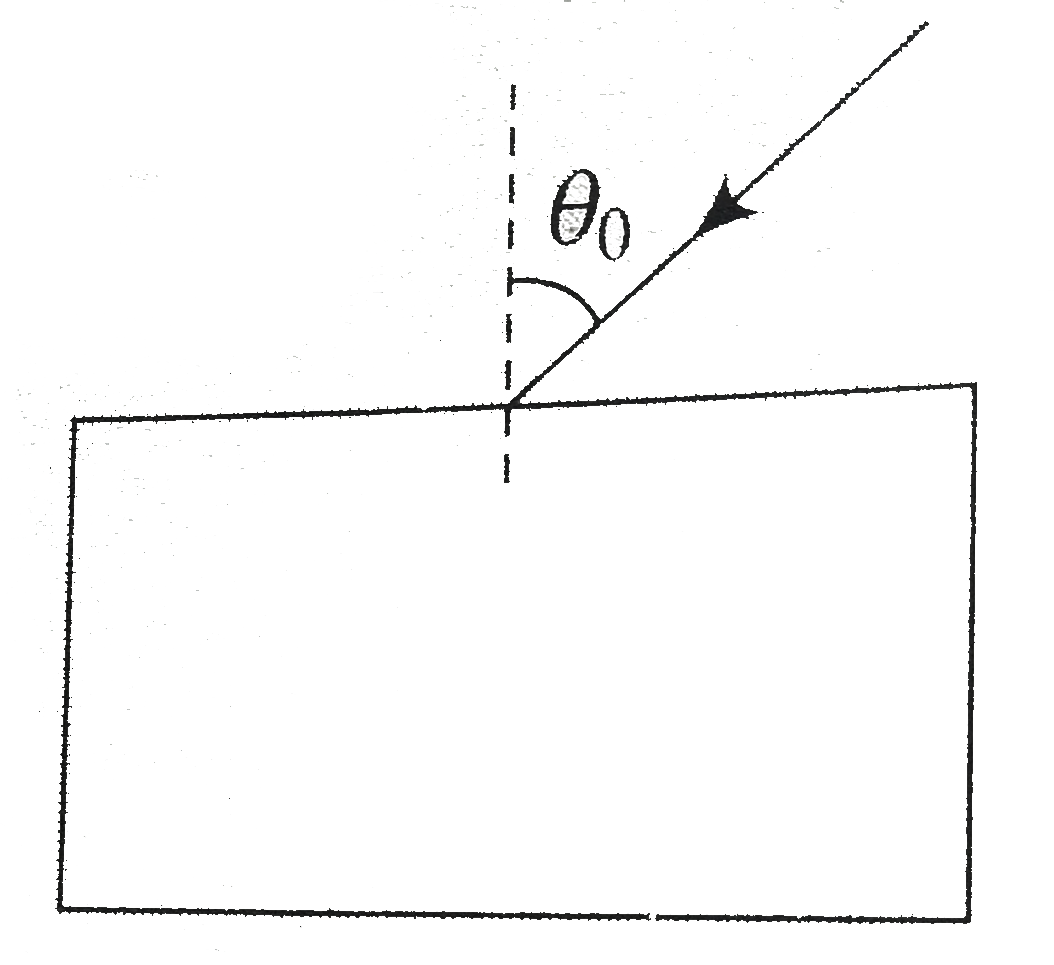
View SolutionA light ray is incident normally on the face AB of a right-angled prism ABC(μ==1.50) as shown in figure. What is the largest angle ϕ for which the light ray is totally reflected at the surface AC ?

View SolutionGiven a slab with index n=1.33 and incident light striking the top horizontal face at angle i as shown in figure. The maximum value of i for which total internal reflection occurs is

View SolutionState the conditions required for total internal reflection of light to take place.
View Solution

