A 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.
The correct Answer is:A
To solve the problem, we need to find the speed of a wave pulse on a string that is subjected to tension due to a block suspended in an accelerating elevator. Here are the steps to find the solution:
Step 1: Identify the forces acting on the block
The block has two forces acting on it:
- The gravitational force (weight) acting downwards, which is given by Fg=mg.
- The tension T in the string acting upwards.
Step 2: Calculate the weight of the block
Given:
- Mass of the block m=4.0kg
- Acceleration due to gravity g=10m/s2
The weight of the block is calculated as:
Fg=mg=4.0kg×10m/s2=40N
Step 3: Apply Newton's second law to find the tension in the string
The elevator is accelerating upwards with an acceleration a=2.0m/s2. According to Newton's second law:
T−Fg=ma
Substituting the known values:
T−40N=4.0kg×2.0m/s2
T−40=8⇒T=40+8=48N
Step 4: Calculate the linear mass density of the string
The linear mass density μ is given as:
μ=19.2×10−3kg/m
Step 5: Use the wave speed formula
The speed of a wave pulse on a string is given by the formula:
v=√Tμ
Substituting the values of tension and linear mass density:
v=√48N19.2×10−3kg/m
Step 6: Simplify the calculation
Calculating the denominator:
19.2×10−3=0.0192kg/m
Now substituting back:
v=√480.0192=√2500=50m/s
Final Answer
The speed with which a wave pulse can proceed on the string is:
50m/s
The block has two forces acting on it:
- The gravitational force (weight) acting downwards, which is given by Fg=mg.
- The tension T in the string acting upwards.
Given:
- Mass of the block m=4.0kg
- Acceleration due to gravity g=10m/s2
Fg=mg=4.0kg×10m/s2=40N
The elevator is accelerating upwards with an acceleration a=2.0m/s2. According to Newton's second law:
T−Fg=ma
Substituting the known values:
T−40N=4.0kg×2.0m/s2
T−40=8⇒T=40+8=48N
The linear mass density μ is given as:
μ=19.2×10−3kg/m
The speed of a wave pulse on a string is given by the formula:
v=√Tμ
Substituting the values of tension and linear mass density:
v=√48N19.2×10−3kg/m
Calculating the denominator:
19.2×10−3=0.0192kg/m
Now substituting back:
v=√480.0192=√2500=50m/s
The speed with which a wave pulse can proceed on the string is:
50m/s
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Question for short Answer
Explore 7 Videos
- WAVE MOTION AND WAVES ON A STRINGBook:HC VERMA ENGLISHChapter:WAVE MOTION AND WAVES ON A STRINGExercise:Objective -2
Explore 9 Videos
- THE FORCESBook:HC VERMA ENGLISHChapter:THE FORCESExercise:Questions for short Answer
Explore 9 Videos
- WORK AND ENERGYBook:HC VERMA ENGLISHChapter:WORK AND ENERGYExercise:Question for Short Answer
Explore 16 Videos
Similar Questions
A heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 60cms−1 on the string when the car is at rest and 62cms−1 when the car accelerates on a horizontal road. Find the acceleration of the car. Take g=10ms−2
View SolutionA transverse wave described by
y=(0.02m)sin[(1.0m−1)x+(30s−1)t]
propagates on a stretched string having a linear mass density of 1.2×10−4kgm−1. Find the tension in the string.
View SolutionA piano string having a mass per unit length equal to 5.00×103kg/m is under a tension of 1350N, Find the speed with which a wave travels on this string.
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
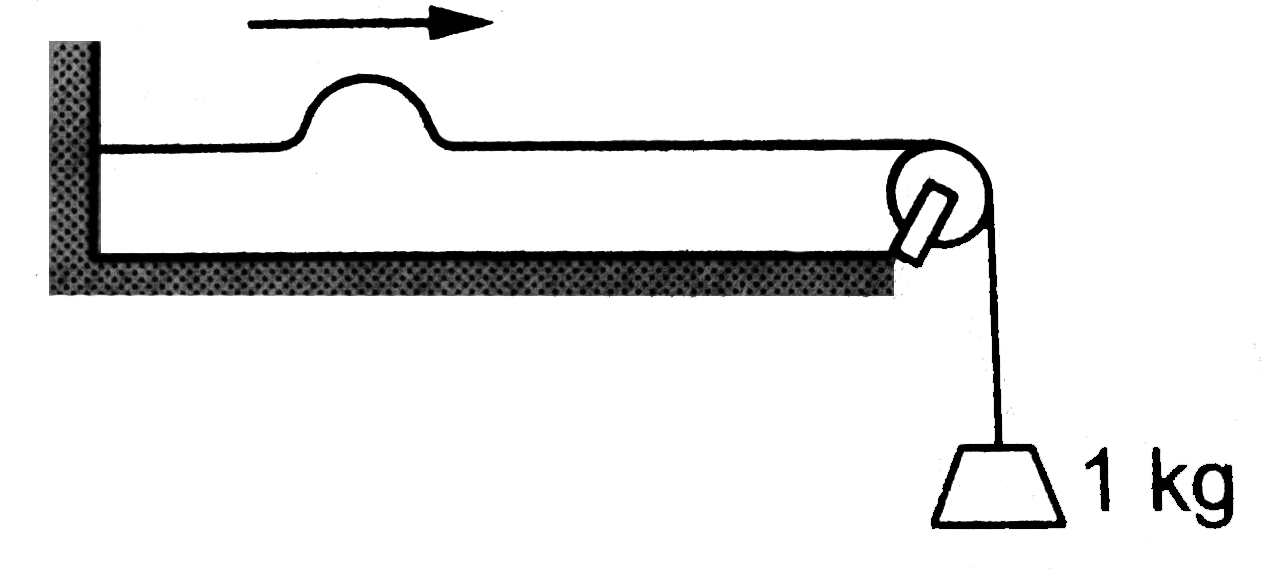
View SolutionFigure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
View SolutionA heavy ball of mass M is suspended from the ceiling of a car by a light string of mass m where m less than M. When the car is at rest, the speed of transverse waves in the string is 60,ms−1.When the car has acceleration a, the wave speed increases to 60.5ms−1.The value of a, in terms of gravitational acceleration g, is closest to :
View SolutionA heavy ball is mass M is suspended from the ceiling of a car by a light string of mass m(m<<M). When the car is at rest, the speed of transverse waves in the string is 60ms−1. When the car has acceleration a, the wave-speed increases to 60.5ms−1. The value of a, in terms of gravitational acceleration g, is closest to:
View SolutionA heavy ball is mass M is suspended from the ceiling of a car by a light string of mass m(m<<M). When the car is at rest, the speed of transverse waves in the string is 60ms−1. When the car has acceleration a, the wave-speed increases to 60.5ms−1. The value of a, in terms of gravitational acceleration g, is closest to:
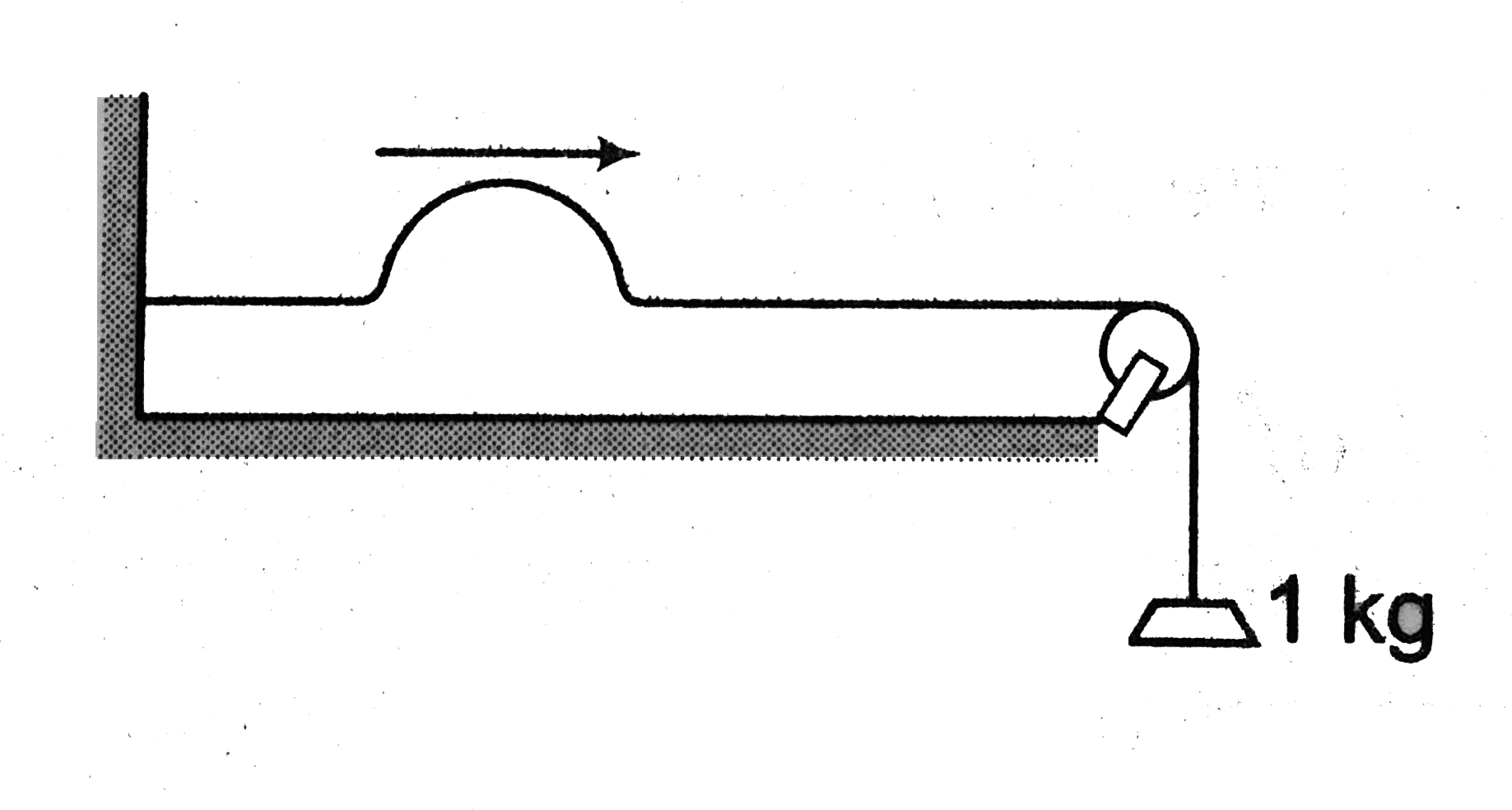
View SolutionFigure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
View SolutionTwo long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
View Solution

