A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass135∘ and surface tension of mercury =0.466Nm−1. Density of mercury=13600kgm−3.
The correct Answer is:C
To solve the problem of determining the height of mercury raised in a barometer tube, we will follow these steps:
Step 1: Understand the Given Values
We have the following values provided in the problem:
- Radius of the tube, r=1.0mm=1.0×10−3m
- Atmospheric pressure equivalent to mercury height, h0=76cm=0.76m
- Contact angle of mercury with glass, θ=135∘
- Surface tension of mercury, σ=0.466N/m
- Density of mercury, ρ=13600kg/m3
- Acceleration due to gravity, g=9.8m/s2
Step 2: Calculate the Capillary Depression
The formula for capillary rise (or depression) is given by:
hc=2σcosθρrg
Where:
- hc is the height of capillary rise (or depression),
- σ is the surface tension,
- θ is the contact angle,
- ρ is the density of the liquid,
- r is the radius of the tube,
- g is the acceleration due to gravity.
Step 3: Calculate cos(135∘)
We need to calculate cos(135∘):
cos(135∘)=−1√2≈−0.7071
Step 4: Substitute the Values into the Formula
Now we can substitute the values into the formula for hc:
hc=2×0.466×(−0.7071)13600×(1.0×10−3)×9.8
Step 5: Calculate hc
Calculating the numerator:
2×0.466×(−0.7071)≈−0.659
Calculating the denominator:
13600×(1.0×10−3)×9.8≈133.28
Now, substituting these values into the equation:
hc=−0.659133.28≈−0.00494m≈−0.494cm
Step 6: Calculate the Height of Mercury in the Barometer Tube
The height of mercury in the barometer tube can be calculated as:
h=h0+hc
Substituting the values:
h=76cm−0.494cm=75.506cm≈75.5cm
Final Answer
The height of mercury raised in the barometer tube is approximately 75.5 cm.
---
We have the following values provided in the problem:
- Radius of the tube, r=1.0mm=1.0×10−3m
- Atmospheric pressure equivalent to mercury height, h0=76cm=0.76m
- Contact angle of mercury with glass, θ=135∘
- Surface tension of mercury, σ=0.466N/m
- Density of mercury, ρ=13600kg/m3
- Acceleration due to gravity, g=9.8m/s2
The formula for capillary rise (or depression) is given by:
- hc is the height of capillary rise (or depression),
- σ is the surface tension,
- θ is the contact angle,
- ρ is the density of the liquid,
- r is the radius of the tube,
- g is the acceleration due to gravity.
We need to calculate cos(135∘):
Now we can substitute the values into the formula for hc:
Calculating the numerator:
The height of mercury in the barometer tube can be calculated as:
The height of mercury raised in the barometer tube is approximately 75.5 cm.
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Question For short Anser
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Worked out Example
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SOUND WAVESBOOK - HC VERMA ENGLISHCHAPTER - SOUND WAVESEXERCISE - All Questions
133 Videos
Similar Questions
Explain how is the height of mercury column in the tube of a simple barometer, a measure of the atmospheric pressure.
View SolutionA satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
View SolutionA satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
View SolutionSuppose the pressure at the surface of mercury in as barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
View SolutionFind the excess pressure inside a mercury drop of radius 2.0 mm. The surface tension of mercury 0.464Nm−1.
View SolutionThe column of mercury in a barometer is 76mm of Hg. Calculate the atmospheric pressure if the density of mercury = 13600kgm −3 . (Take g=10ms −2 )
View SolutionThe tube of a mercury barometer is 4.5 mm in diameter . What error does surface tension introduce in the reading? Given angle of contact of mercury and glass is 140∘. Surface tension of mercury 54×10−2Nm−1 and density 13.6 g m / cc .
View SolutionMercury in a capillary tube is depressed by 1.16cm. The diameter of the capillary tube is 1mm. Calculate the angle of contact of mercury with the glass if the surface tension of mercury is 54×10Nm−1 and its density is 13.6×103kgm−3.
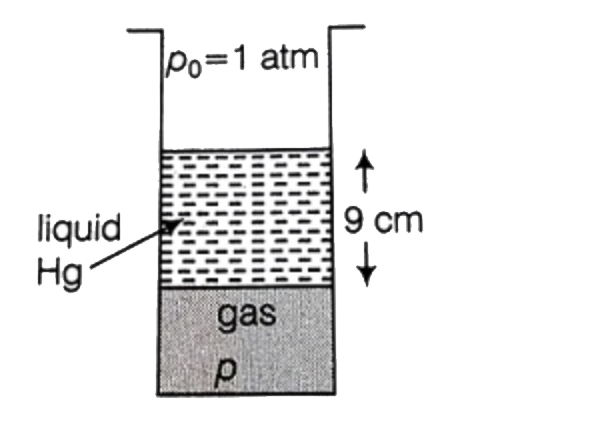
View SolutionIn the given figure, atmospheric pressure p0=1 atm and mercury column length is 9 cm. Pressure p of the gas enclosed in the tube is
View SolutionThe lower end of a capillary tube of radius 1 mm is dipped vertically into mercury. (a) Find the depression of mercury column in the capillary. (b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertical. Surface tension of mercury =0.465Nm−1 and the contact angle of mercury with glass =135∘.
View Solution
