Find the dimensions of
a. electric field E,
magnetic field B and
magnetic permeability μ0
. The relavant equations are
F=qE,FqvB,andB=μ0I2πα,
where F is force q is charge, ν is speed I is current, and α is distance.
The correct Answer is:A, B, C
To find the dimensions of the electric field (E), magnetic field (B), and magnetic permeability (μ₀), we will use the relevant equations provided.
Step 1: Find the dimensions of the electric field (E)
1. Start with the equation for force:
F=qE
Rearranging gives:
E=Fq
2. We know the dimensions of force (F) are:
(F)=M1L1T−2
3. The charge (q) can be expressed in terms of current (I) and time (T):
q=I⋅T
Therefore, the dimensions of charge are:
(q)=A1T1
4. Substitute the dimensions of F and q into the equation for E:
(E)=(F)(q)=M1L1T−2A1T1
5. Simplifying this gives:
(E)=M1L1T−3A−1
Step 2: Find the dimensions of the magnetic field (B)
1. Start with the equation:
F=qvB
Rearranging gives:
B=Fqv
2. We already have the dimensions for F and q. The velocity (v) can be expressed as distance over time:
v=LT
Therefore, the dimensions of velocity are:
(v)=L1T−1
3. Substitute the dimensions into the equation for B:
(B)=(F)(q)(v)=M1L1T−2(A1T1)(L1T−1)
4. Simplifying this gives:
(B)=M1L0T−2A−1
Step 3: Find the dimensions of magnetic permeability (μ₀)
1. Use the equation:
B=μ0I2πα
Rearranging gives:
μ0=B⋅2παI
2. The dimensions of α (distance) are:
(α)=L1
3. Substitute the dimensions into the equation for μ₀:
(μ0)=(B)⋅(α)(I)=(M1L0T−2A−1)(L1)A1
4. Simplifying this gives:
(μ0)=M1L1T−2A−2
Final Results
- Dimensions of electric field (E): M1L1T−3A−1
- Dimensions of magnetic field (B): M1L0T−2A−1
- Dimensions of magnetic permeability (μ₀): M1L1T−2A−2
F=qE
Rearranging gives:
E=Fq
(F)=M1L1T−2
q=I⋅T
Therefore, the dimensions of charge are:
(q)=A1T1
(E)=(F)(q)=M1L1T−2A1T1
(E)=M1L1T−3A−1
F=qvB
Rearranging gives:
B=Fqv
v=LT
Therefore, the dimensions of velocity are:
(v)=L1T−1
(B)=(F)(q)(v)=M1L1T−2(A1T1)(L1T−1)
(B)=M1L0T−2A−1
B=μ0I2πα
Rearranging gives:
μ0=B⋅2παI
(α)=L1
(μ0)=(B)⋅(α)(I)=(M1L0T−2A−1)(L1)A1
(μ0)=M1L1T−2A−2
- Dimensions of electric field (E): M1L1T−3A−1
- Dimensions of magnetic field (B): M1L0T−2A−1
- Dimensions of magnetic permeability (μ₀): M1L1T−2A−2
Topper's Solved these Questions
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 2
3 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMA ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions
106 Videos
Similar Questions
The dimension of B22μ0, where B is magnetic field and μ0 is the magnetic permeability of vacuum, is :
View SolutionFind the dimensions of
a. electric dipole moment p and
b. magnetic dipole moment M.
The defining equations are p=q.dandM=IA,
whre d is distance, A is area, q is charge and I is current.
View SolutionA charge q moves region in a electric field E and the magnetic field B both exist, then the force on its is
View SolutionE2μ0 has the dimensions (E= electric field, μ0= permeabililty of free space)
View SolutionThe dimensions of B2R2C22μ0 (Where B is magnetic filed, and μ0 is permeability of free space , R resistance and C is capacitance) is
View SolutionEnergy density in the electric field of electromagnetic wave is U.If amplitude of electric field (E0) and magnetic field (B0) is related as E0=cB0, then energy density in magnetic field is(c = speed of light)
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
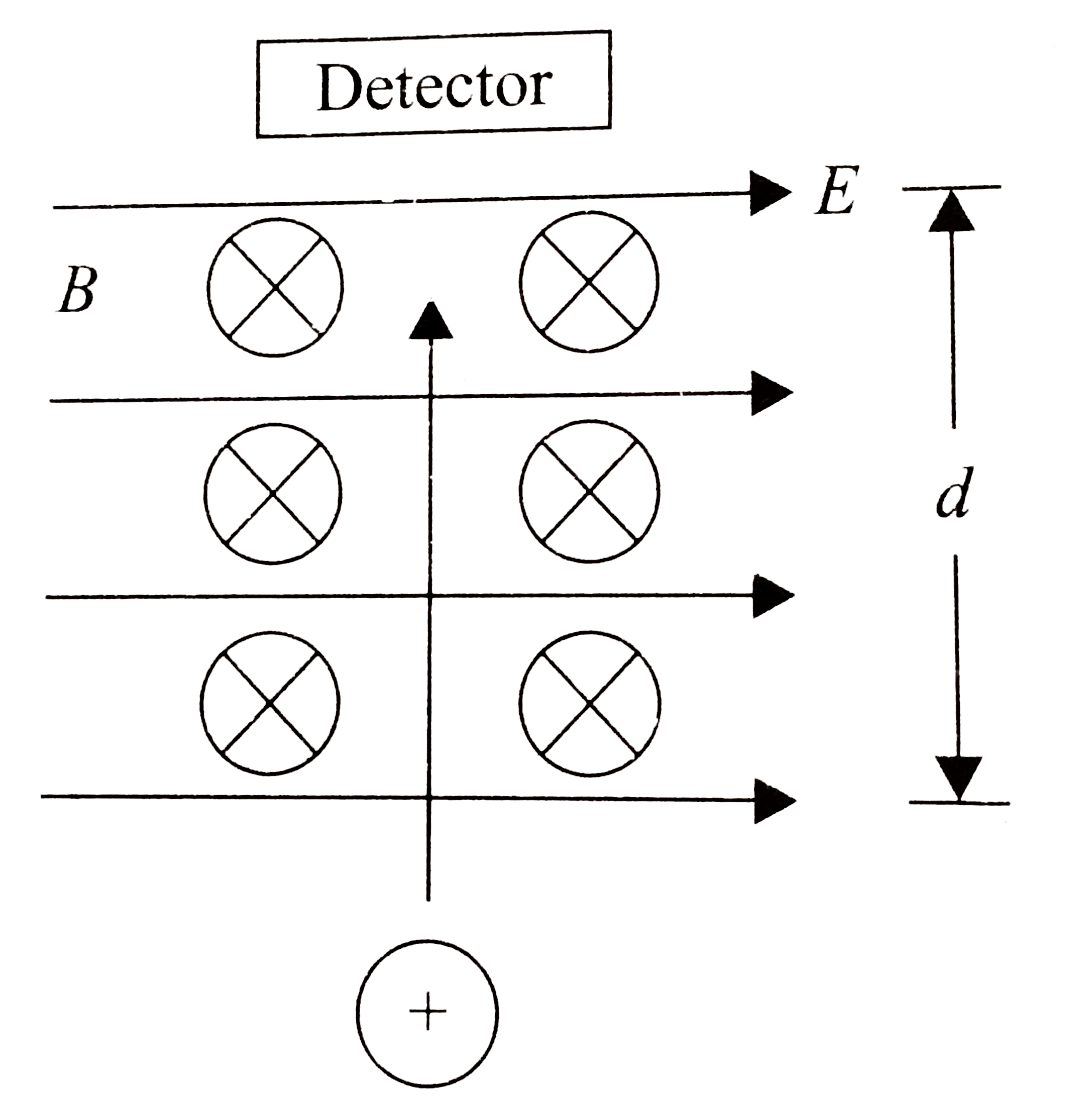
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
View SolutionA He2+ at rest experiences an electromagnetic force. Then (where E is electric field and is B magnetic field)
View SolutionConsider the equation F=a2be−bxE where F is force x is distance E is energy and a, b are constants. What are the dimensions of a and b?
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.

View Solution
