Choose the correct statement(s)
All quantities may be represented dimensionally in terms of the base quantities
A base quantity cannot be represented dimensionally in terms of the rest of the base quantities
The dimension of a base quantity in other base quantities is always zero.
The dimension of a derived quantity is never zero in any base quantity.
The correct Answer is:A, B, C
To solve the problem, we need to analyze each of the statements provided and determine their correctness based on the principles of dimensional analysis.
1. Statement A: All quantities may be represented dimensionally in terms of the base quantities.
- Analysis: Base quantities include mass (M), length (L), time (T), current (I), amount of substance (mol), temperature (K), and luminous intensity (cd). Derived quantities can be expressed in terms of these base quantities. For example, charge (Q) can be expressed as current (I) multiplied by time (T), giving dimensions of IT. Similarly, pressure (P) can be expressed as force (F) per unit area (A), where F has dimensions of ML^1T^-2 and A has dimensions of L^2, leading to P = F/A = ML^-1T^-2.
- Conclusion: This statement is correct.
2. Statement B: A base quantity cannot be represented dimensionally in terms of the rest of the base quantities.
- Analysis: Base quantities are fundamental and cannot be expressed in terms of each other. For instance, mass (M) cannot be expressed in terms of length (L) or time (T). Each base quantity is independent.
- Conclusion: This statement is correct.
3. Statement C: The dimension of a base quantity in other base quantities is always 0.
- Analysis: When expressing a base quantity in terms of itself, it has a dimension of 1, and in terms of all other base quantities, it has a dimension of 0. For example, the dimension of length (L) can be expressed as M^0L^1T^0I^0mol^0K^0cd^0, where all other dimensions are 0.
- Conclusion: This statement is correct.
4. Statement D: The dimension of a derived quantity is never 0 in any base quantity.
- Analysis: Derived quantities can have dimensions that are zero in terms of certain base quantities. For example, the dimension of pressure (P) is ML^-1T^-2, which means it has non-zero dimensions in mass, length, and time, but it has zero dimensions in terms of amount of substance (mol), luminous intensity (cd), and absolute temperature (K).
- Conclusion: This statement is false.
Final Conclusion:
- The correct statements are A, B, and C. Statement D is incorrect.
- Analysis: Base quantities include mass (M), length (L), time (T), current (I), amount of substance (mol), temperature (K), and luminous intensity (cd). Derived quantities can be expressed in terms of these base quantities. For example, charge (Q) can be expressed as current (I) multiplied by time (T), giving dimensions of IT. Similarly, pressure (P) can be expressed as force (F) per unit area (A), where F has dimensions of ML^1T^-2 and A has dimensions of L^2, leading to P = F/A = ML^-1T^-2.
- Conclusion: This statement is correct.
- Analysis: Base quantities are fundamental and cannot be expressed in terms of each other. For instance, mass (M) cannot be expressed in terms of length (L) or time (T). Each base quantity is independent.
- Conclusion: This statement is correct.
- Analysis: When expressing a base quantity in terms of itself, it has a dimension of 1, and in terms of all other base quantities, it has a dimension of 0. For example, the dimension of length (L) can be expressed as M^0L^1T^0I^0mol^0K^0cd^0, where all other dimensions are 0.
- Conclusion: This statement is correct.
- Analysis: Derived quantities can have dimensions that are zero in terms of certain base quantities. For example, the dimension of pressure (P) is ML^-1T^-2, which means it has non-zero dimensions in mass, length, and time, but it has zero dimensions in terms of amount of substance (mol), luminous intensity (cd), and absolute temperature (K).
- Conclusion: This statement is false.
- The correct statements are A, B, and C. Statement D is incorrect.
Topper's Solved these Questions
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 1
6 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMA ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions
106 Videos
Similar Questions
A curved surface of radius R separates two medium of refractive indices μ1andμ2 as shown in figures A and B .
_E01_077_Q01.png)
Choose the correct statement(s) related to the real image formed by the object O placed at a distance x, as shown in figure A.
View SolutionA curved surface of radius R separates two medium of refractive indices μ1andμ2 as shown in figures A and B .
_E01_078_Q01.png)
Choose the correct statement(s) related to the virtual image formed by object O placed at a distance x, as shown in figure
View SolutionChoose the correct statements(s):
View SolutionConsider the following compounds:
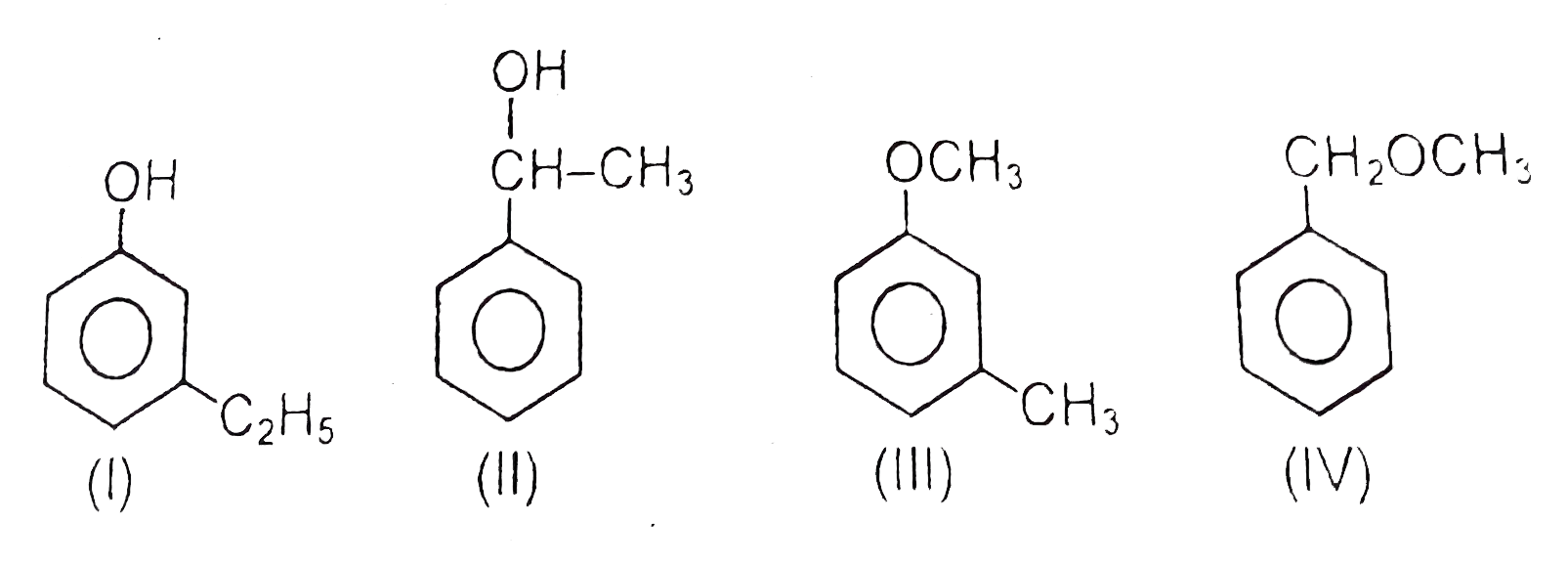
Choose the correct statements(s) from the following:
View Solution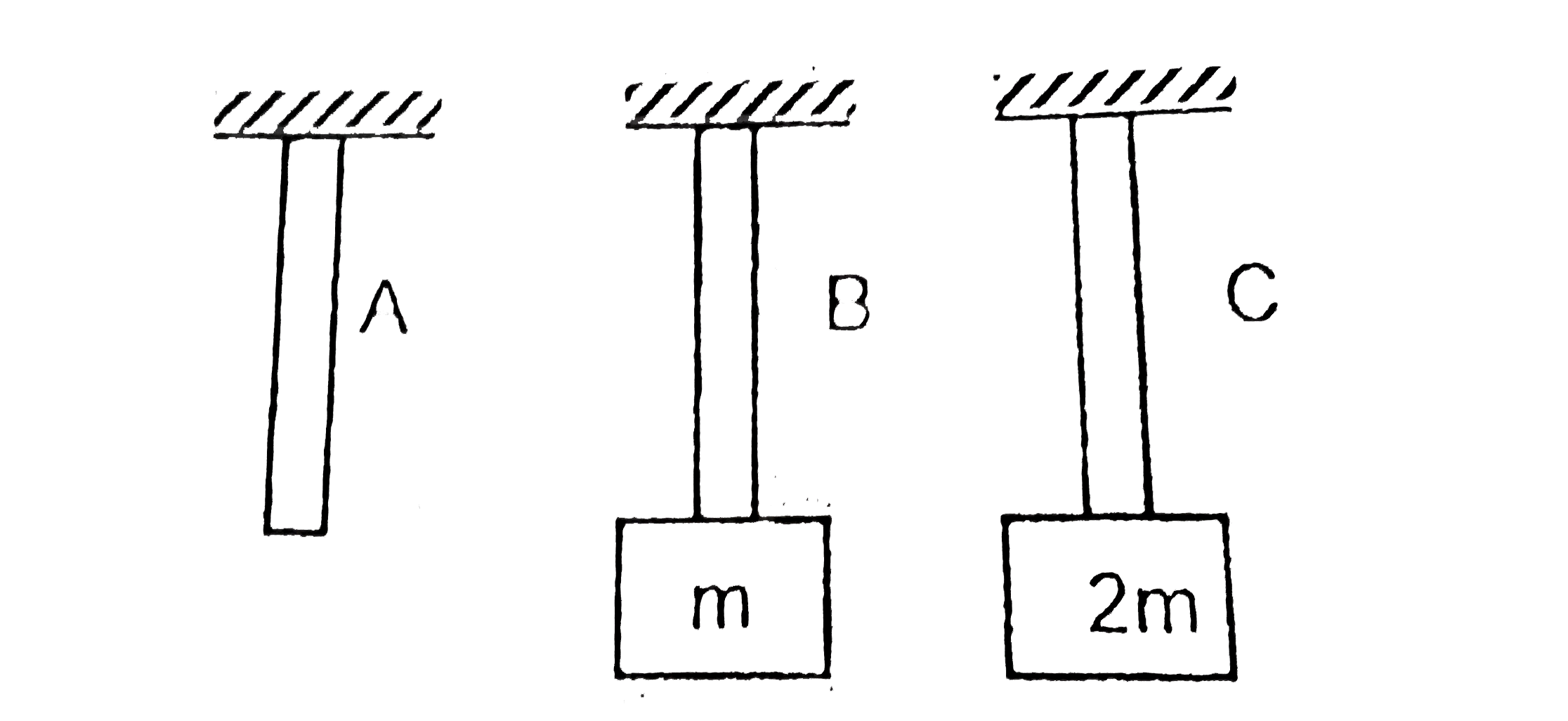
Consider the three ropes of same length and same linear density as (shown in figure) suspended from the ceiling.
A pulse is generated at the lowest point of the three ropes simultaneously. Choose the correct statements(s)
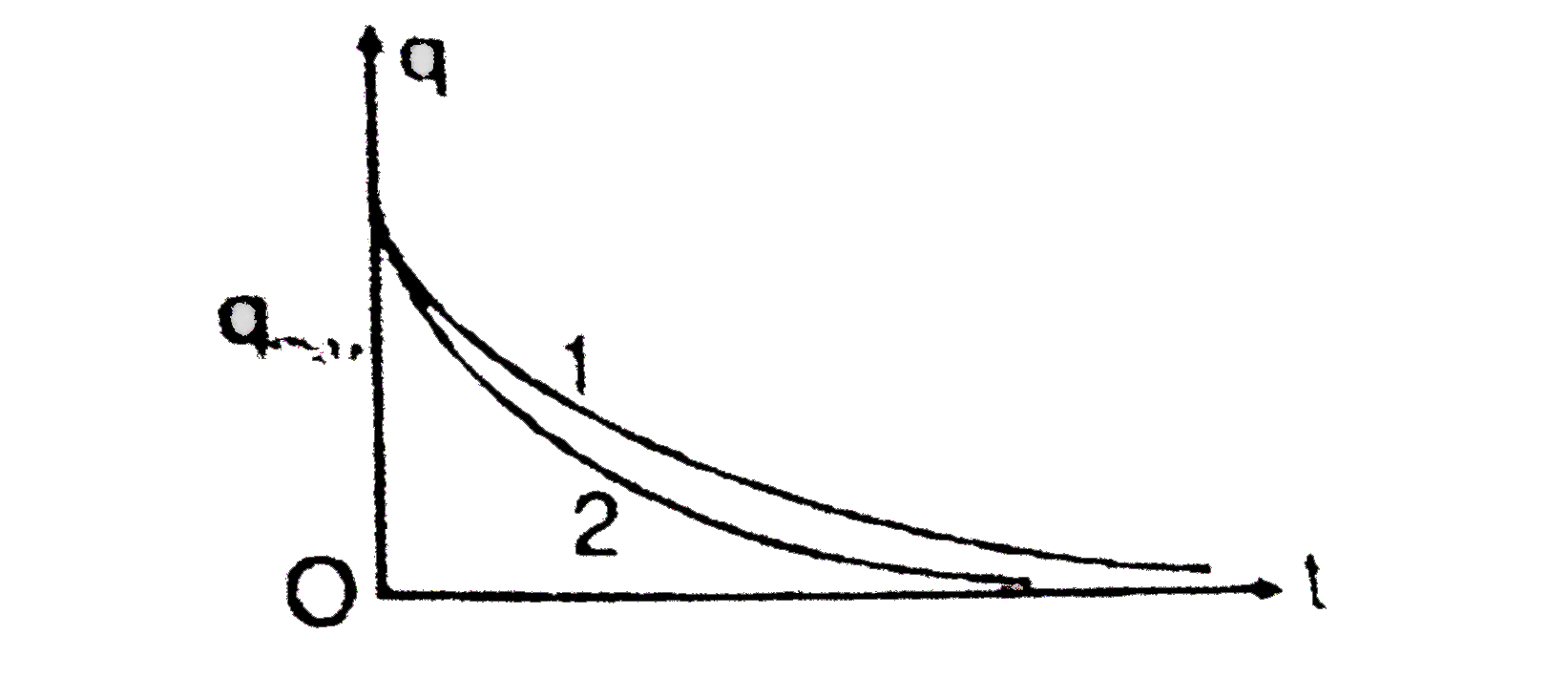
View SolutionThe instantaneous charge on capacitor in two discharging RC circuils is plotted with respect to time in figure. Choose the correct statement (s) (where E1 and E2 are emfs of two DC sources in two different charging circuits and capacitors are fully charged ).
View Solution
In the adjacent figure blocks A and B of weight W each are lying at rest on a rough horizontal surface. They are pulled by applying forces F1 and F2 as shown in figure. When blocks are in limiting equilibrium F2=5F1 Choose the correct statement (s) (Assume same coefficient of friction for both the blocks)
View SolutionChoose the correct statements.
View SolutionChoose the correct statements
View SolutionThe temperature coefficient of the cell is (∂E∂T)P. Choose the correct statements (s).
View Solution
