If the centripetal force is of the form mavbrc, find the valus of a,b, and c.
To solve the problem of finding the values of a, b, and c in the expression for centripetal force of the form F=mavbrc, we will follow these steps:
Step 1: Write down the dimensions of force
The left-hand side (LHS) of the equation represents force. The dimension of force in terms of mass (M), length (L), and time (T) is given by:
(F)=kg⋅m/s2=(M)(L)(T−2)
Thus, the dimension of force is:
(F)=(M1L1T−2)
Step 2: Write down the dimensions of the right-hand side
The right-hand side (RHS) is given as mavbrc. We will express the dimensions of each variable:
- Mass m has the dimension (M).
- Velocity v has the dimension (LT−1).
- Distance r has the dimension (L).
Now, substituting these dimensions into the RHS:
(ma)=(Ma)
(vb)=(LbT−b)
(rc)=(Lc)
Combining these, we get:
(RHS)=(MaLb+cT−b)
Step 3: Set the dimensions of LHS equal to RHS
For the equation to hold true, the dimensions on both sides must be equal:
(M1L1T−2)=(MaLb+cT−b)
Step 4: Compare the dimensions
Now we can compare the powers of M, L, and T from both sides:
1. For mass M:
a=1
2. For length L:
b+c=1
3. For time T:
−b=−2⟹b=2
Step 5: Solve for c
Now that we have b=2, we can substitute this value into the equation for length:
b+c=1⟹2+c=1⟹c=1−2=−1
Conclusion
Thus, the values of a, b, and c are:
a=1,b=2,c=−1
Final Answer
The final answer is:
a=1,b=2,c=−1
---
The left-hand side (LHS) of the equation represents force. The dimension of force in terms of mass (M), length (L), and time (T) is given by:
(F)=kg⋅m/s2=(M)(L)(T−2)
Thus, the dimension of force is:
(F)=(M1L1T−2)
The right-hand side (RHS) is given as mavbrc. We will express the dimensions of each variable:
- Mass m has the dimension (M).
- Velocity v has the dimension (LT−1).
- Distance r has the dimension (L).
(ma)=(Ma)
(vb)=(LbT−b)
(rc)=(Lc)
(RHS)=(MaLb+cT−b)
For the equation to hold true, the dimensions on both sides must be equal:
(M1L1T−2)=(MaLb+cT−b)
Now we can compare the powers of M, L, and T from both sides:
a=1
b+c=1
−b=−2⟹b=2
Now that we have b=2, we can substitute this value into the equation for length:
b+c=1⟹2+c=1⟹c=1−2=−1
Thus, the values of a, b, and c are:
a=1,b=2,c=−1
The final answer is:
a=1,b=2,c=−1
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 16videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Objective 23videos
INTRODUCTION TO PHYSICS
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER11videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions106videos
KINETIC THEORY OF GASES
Similar Questions
Find the values of A,B and C
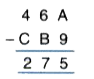 View Solution
View Solution(a) How does a centripetal force differ from a centrifugal force with reference to the direction in which they act?
(b) Is centrifugal force the force of reaction of the centripetal force?
( c) compare the magnitudes of centripetal and centrifugal force.View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
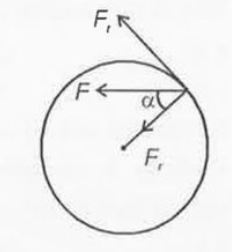 View Solution
View SolutionIf a = 4, b = -5, c = -8, find the value of (a+b)×c.
View SolutionIf a, b, c are distinct positive prime integers such that a2b3c4=49392, find the value of a, b and c
View SolutionIf the numbers a,b,c,d,e form an A.P. , then find the value of a−4b+6c−4d+e.
View SolutionIf the centroid of the triangle formed by points P(a, b), Q(b, c) and R(c, a) is at the origin, what is the value of a+b+c ?
View SolutionIf the centroid of the triangle formed by points P ( a , b ) , Q ( b , c ) and R ( c , a ) is at the origin, what is the value of a2bc+b2ca+c2ab ?
View Solutiona,b,c are three complex numbers on the unit circle |z|=1, such that abc=a+b+⋅ Then find the value of |ab+bc+ca|.
View SolutionIf a+b+c=0 and a2+b2+c2=16 , find the value of ab+bc+ca
View Solution
