Three sets of English, Hindi and Mathematics books have to be stacked in such a way that all the books are stored topic wise and the height of each stack is the same. The number of English books is 96, the number of Hindi books is 240 and the number of Mathematics books is 336. Assuming that the books are of the same thickness, determine the number of stacks of English, Hindi and Mathematics books.
To solve the problem of stacking the English, Hindi, and Mathematics books such that the height of each stack is the same, we need to find the highest common factor (HCF) of the number of books in each subject. Here’s a step-by-step solution:
Step 1: Identify the number of books
- English books: 96
- Hindi books: 240
- Mathematics books: 336
Step 2: Find the prime factorization of each number
1. English books (96):
- 96 ÷ 2 = 48
- 48 ÷ 2 = 24
- 24 ÷ 2 = 12
- 12 ÷ 2 = 6
- 6 ÷ 2 = 3
- 3 ÷ 3 = 1
- Prime factorization: 96=25×31
2. Hindi books (240):
- 240 ÷ 2 = 120
- 120 ÷ 2 = 60
- 60 ÷ 2 = 30
- 30 ÷ 2 = 15
- 15 ÷ 3 = 5
- 5 ÷ 5 = 1
- Prime factorization: 240=24×31×51
3. Mathematics books (336):
- 336 ÷ 2 = 168
- 168 ÷ 2 = 84
- 84 ÷ 2 = 42
- 42 ÷ 2 = 21
- 21 ÷ 3 = 7
- 7 ÷ 7 = 1
- Prime factorization: 336=24×31×71
Step 3: Determine the HCF
- From the prime factorizations:
- English: 25×31
- Hindi: 24×31×51
- Mathematics: 24×31×71
- The HCF is found by taking the lowest power of each common prime factor:
- For 2: the minimum is 24
- For 3: the minimum is 31
Thus, the HCF = 24×31=16×3=48.
Step 4: Calculate the number of stacks for each subject
1. English books:
- Total books = 96
- Number of stacks = 9648=2
2. Hindi books:
- Total books = 240
- Number of stacks = 24048=5
3. Mathematics books:
- Total books = 336
- Number of stacks = 33648=7
Final Answer:
- Number of stacks of English books: 2
- Number of stacks of Hindi books: 5
- Number of stacks of Mathematics books: 7
---
- English books: 96
- Hindi books: 240
- Mathematics books: 336
1. English books (96):
- 96 ÷ 2 = 48
- 48 ÷ 2 = 24
- 24 ÷ 2 = 12
- 12 ÷ 2 = 6
- 6 ÷ 2 = 3
- 3 ÷ 3 = 1
- Prime factorization: 96=25×31
- 240 ÷ 2 = 120
- 120 ÷ 2 = 60
- 60 ÷ 2 = 30
- 30 ÷ 2 = 15
- 15 ÷ 3 = 5
- 5 ÷ 5 = 1
- Prime factorization: 240=24×31×51
- 336 ÷ 2 = 168
- 168 ÷ 2 = 84
- 84 ÷ 2 = 42
- 42 ÷ 2 = 21
- 21 ÷ 3 = 7
- 7 ÷ 7 = 1
- Prime factorization: 336=24×31×71
- From the prime factorizations:
- English: 25×31
- Hindi: 24×31×51
- Mathematics: 24×31×71
- For 2: the minimum is 24
- For 3: the minimum is 31
1. English books:
- Total books = 96
- Number of stacks = 9648=2
- Total books = 240
- Number of stacks = 24048=5
- Total books = 336
- Number of stacks = 33648=7
- Number of stacks of English books: 2
- Number of stacks of Hindi books: 5
- Number of stacks of Mathematics books: 7
Topper's Solved these Questions
Similar Questions
Two sets of English and social science books containing 336 and 96 respectively in a library have to be stacked in such a way that an the books are stored topic wise and the height of each stack is the same. Assuming that the books are of the same thickness, determine the number of stacks. What are the characteristics of library?
View SolutionEleven books are stacked on top of each other. If each book is 2.35 cm thick, find the height of the stack.
View Solution
Knowledge Check
The number of ways in which 4 books of Mathematics and 3 books of English can be placed in a shelf, so that the books on the same subject always remain together is
A144B210C288D372
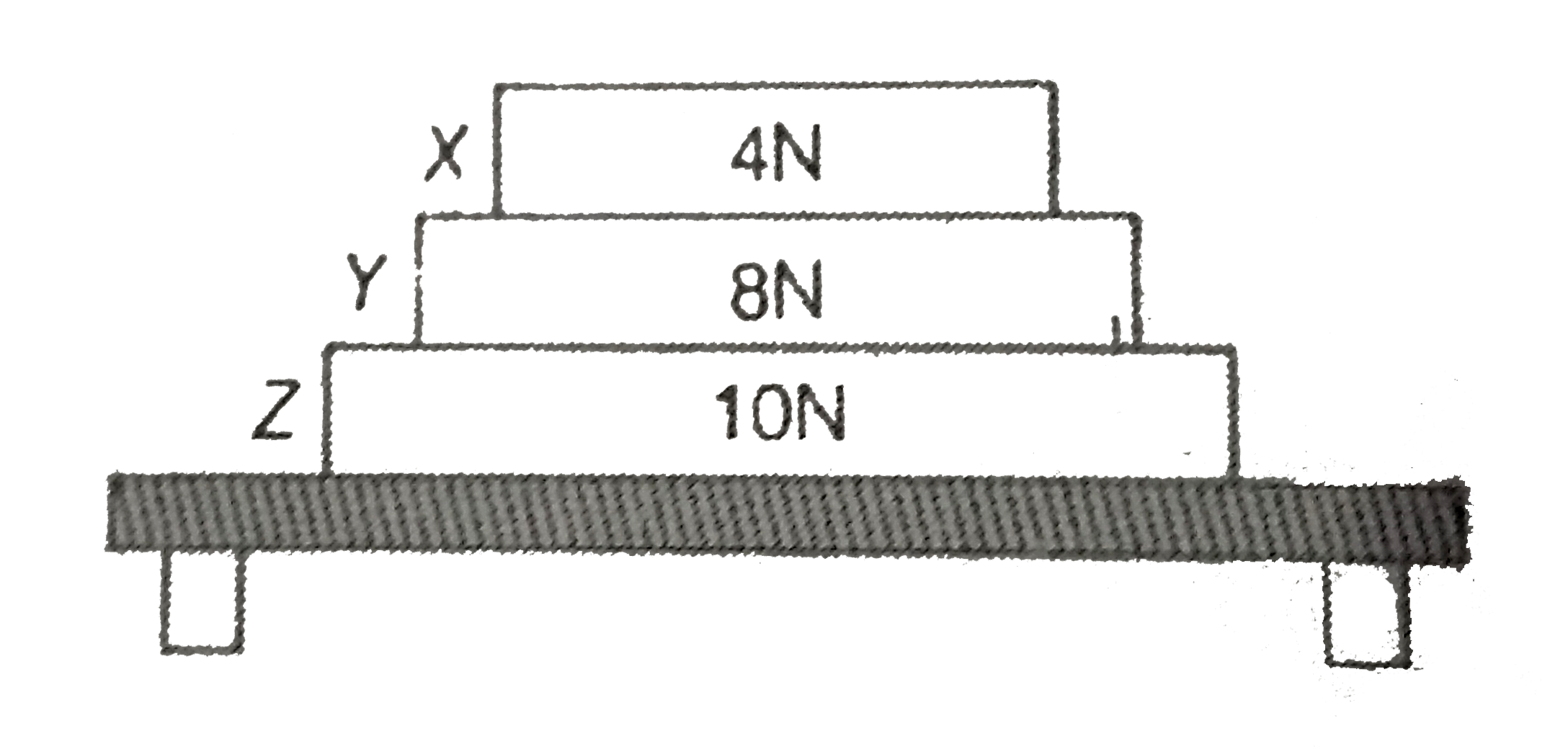
Three books (X,Y and Z) rest on a table. The weight of each book is indicated. The net force acting on book Y is
View SolutionThe weight of 72 books is 9 kg. What is the weight of 40 such books?
View SolutionIf 4 books cost रु 270.6, find the cost of one book.
View SolutionThe ratio of storybooks in a library to other books is 1:7. The total number of story books is 800. Find the total number of books in the library.
View SolutionIn a school library, the ratio of mathematics books to Science books is the same as the ratio of Science books to Hindi books. If there are 450 books in Science and 300 books in Hindi, find the number of books in Mathematics.
View SolutionIn the school cupboard, 36 math books were stacked one on top of the other. If each maths book is 213cm thick, what is the height of the stack of books?
View SolutionThe cost of Mathematics book is Rs 2534 and that of Science book is Rs 2012. Which costs more and by how much?
View Solution

