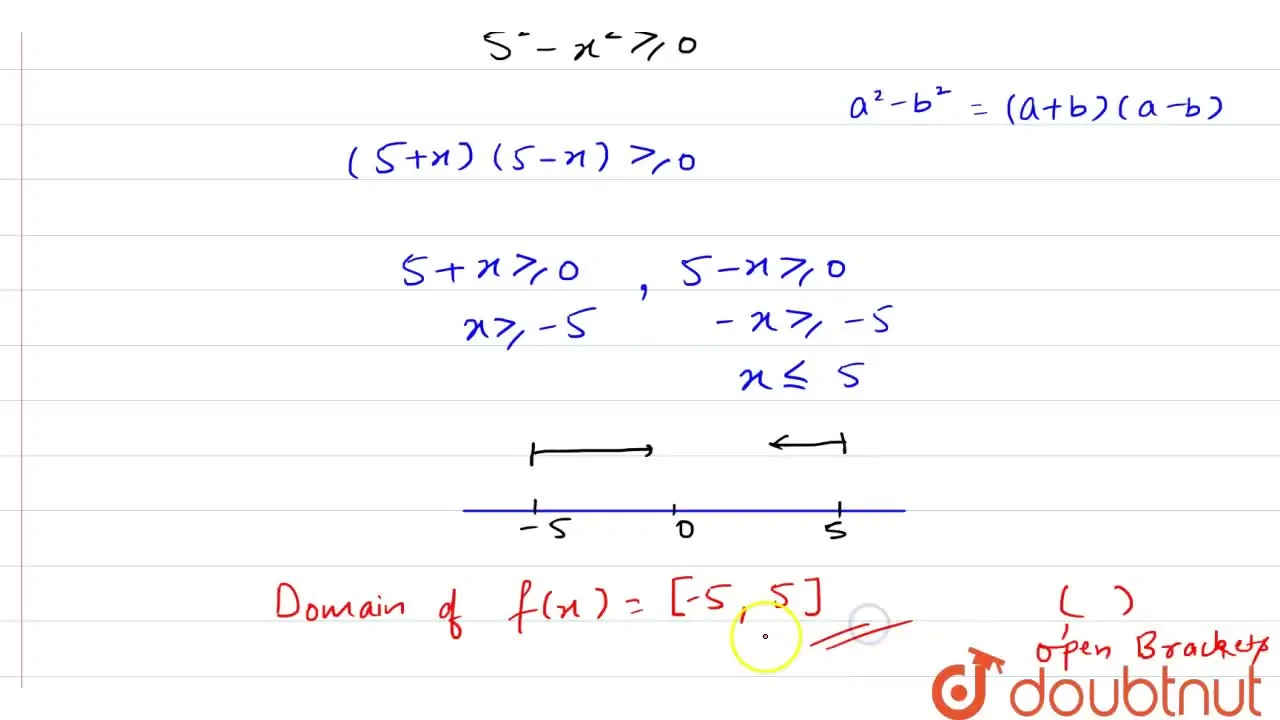
Write the domain of the real function f defined by f(x)=√25−x2 .
Step by step video & image solution for Write the domain of the real function f defined by f(x)=sqrt(25-x^2) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Let D be the domain of the real valued function f defined by f(x)=√25−x2 . Then, write D.
View SolutionThe domain of the function f defined by f(x)=√x2−9 is
View SolutionFind the domain of the real function f(x) defined by f(x)=√1−|x|2−|x|.
View SolutionThe domain of the function f defined by f(x)=1√|x|−x is
View SolutionFind the domain and the range of the real function f defined by f(x)=√(x−1).
View SolutionFind the domain and the range of the real function f defined by f(x)=√(x−1).
View SolutionFind the domain and the range of the real function f defined by f(x)=√(x−1).
View SolutionThe domain of the fiction f defined by f(x)=l√9−x2 is
View SolutionFind the domain and the range of the real function f defined by f(x)=√(x−1).(a)Domain = ( 1 , ∞ ) , Range = ( 0 , ∞ ) (b) Domain = [ 1 , ∞ ) , Range = ( 0 , ∞ (c) Domain = ( 1 , ∞ ) , Range = [ 0 , ∞ ) (d)Domain = [ 1 , ∞ ) , Range = [ 0 , ∞ )
View SolutionThe domain of the function defined by f(x)=sin−1√x−1 is
View Solution