Fill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are...
Step by step video & image solution for Fill in the blanks in each of the following to make the statement true: (i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are.... (ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are... by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
Which of the following statements are true (T) and which are false (F)? Give reasons.
(i)If two lines are intersected by a transversal, then corresponding angles are equal.
(ii)If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
(iii)Two lines perpendicular to the same line are perpendicular to each other.
(iv)Two lines parallel to the same line are parallel to each other.
(v)If two parallel lines are intersected by a transversal, then the interior angle on the same side of the transversal are equal.View SolutionTheorem 6.4 : If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
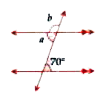 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
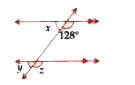 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
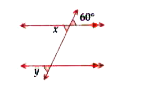 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
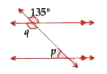 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
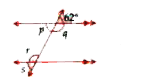 View Solution
View SolutionIn the following figures (i) to (iv), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle
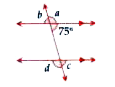 View Solution
View Solution


