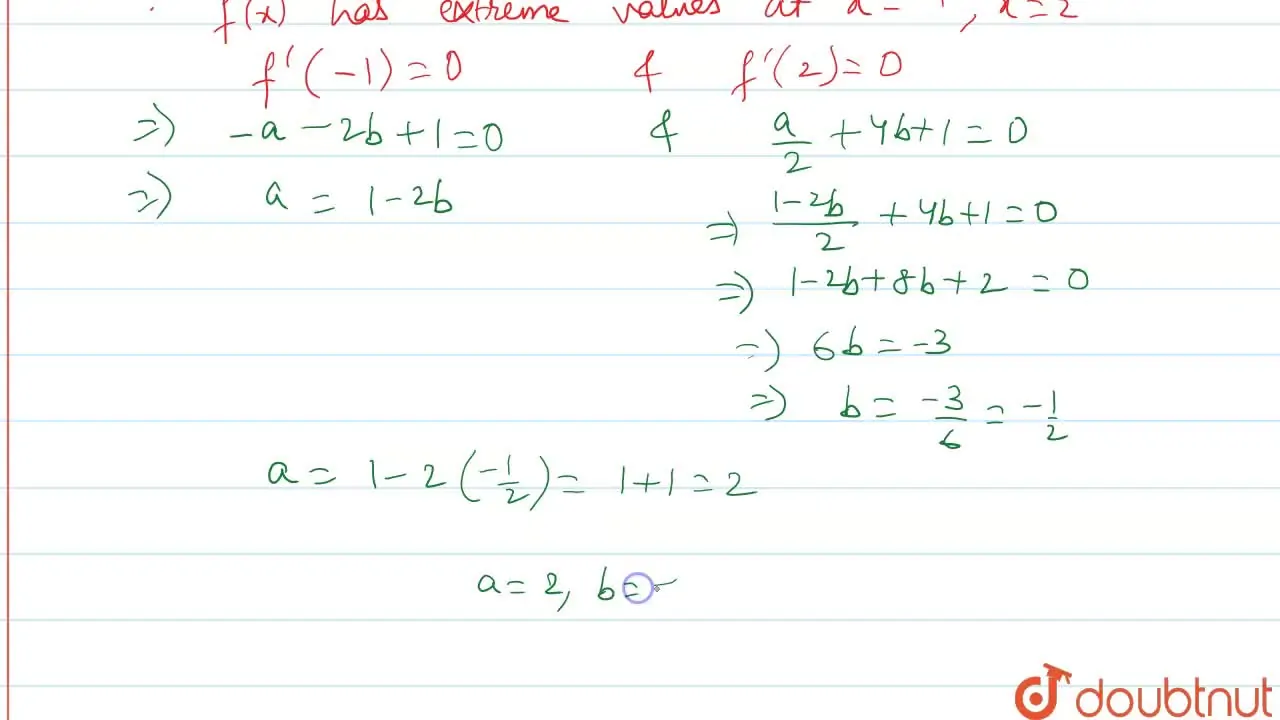If f(x)=alog|x|+bx2+x has extreme values at x=−1 and at x=2, then find a and b .
Step by step video & image solution for If f(x)=alog|x|+b x^2+x has extreme values at x=-1 a n d a t x=2, then find a and b . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
If f(x)=alog|x|+bx2+x has extreme values at x=−1 and at x=2 , then find a and b .
View SolutionThe function y=alogx+bx2+x has extreme values at x=1 and x=2 . Find a and b .
View SolutionIf f(x) =X3+ax2+bx+c has extreme values at x=-1 and x=3 . Find a,b,c.
View SolutionThe function y=alogx+bx2+x has extreme values at x=1,2.Find a and b
View SolutionIf the function f(x) =axebx2 has maximum value at x=2 such that f(2) =1 , then find the values of a and b
View SolutionIf f(x)=x3+ax2+bx+c has a maximum at x = -1 and minimum at x = 3. Find a + b.
View SolutionIf the maximum value of ||x−3|−|x−2∣∣ is a and minimum value of |x−1|+|x−2| is b, then find the value of (a+b).
View SolutionIf h(x)=f(x)+f(-x), " then " h(x) has got and extreme value at a point where f'(x) is
View SolutionThe function f(x)=√ax3+bx2+cx+d has its non-zero local minimum and local maximum values at x=−2andx=2, respectively. If a is a root of x2−x−6=0, then find a,b,c and d.
View SolutionLet f(x)=(x−14)(x−2n),n∈N.Then f(x) has
View Solution