PQ and RS are two parallel chords of a circle whose centre is O and radius is 10cm. If PQ=16cm and RS=12cm, find the distance between PQ and RS, if they lie: on the same side of the centre O. on opposite side of the centre O.
To solve the problem, we need to find the distance between the two parallel chords PQ and RS of a circle with a radius of 10cm. We are given that the lengths of the chords are PQ=16cm and RS=12cm. We will solve this for two cases: when the chords are on the same side of the center O and when they are on opposite sides.
1. Identify the half-lengths of the chords:
- For chord PQ:
PT=PQ2=162=8cm
- For chord RS:
RV=RS2=122=6cm
2. Apply the Pythagorean theorem:
- For triangle OPT (where O is the center, P is one endpoint of the chord PQ, and T is the foot of the perpendicular from O to PQ):
OP2=OT2+PT2
102=H21+82
100=H21+64
H21=100−64=36⇒H1=6cm
- For triangle ORV (where R is one endpoint of the chord RS, and V is the foot of the perpendicular from O to RS):
OR2=OV2+RV2
102=H22+62
100=H22+36
H22=100−36=64⇒H2=8cm
3. Calculate the distance between the chords:
- Since both chords are on the same side of the center:
Distance=H2−H1=8−6=2cm
Case 2: Chords on Opposite Sides of the Center
1. Use the same heights calculated:
- H1=6cm
- H2=8cm
2. Calculate the distance between the chords:
- Since the chords are on opposite sides of the center:
Distance=H1+H2=6+8=14cm
Final Answers:
- Distance when both chords are on the same side: 2 cm
- Distance when both chords are on opposite sides: 14 cm
- For chord PQ:
PT=PQ2=162=8cm
- For chord RS:
RV=RS2=122=6cm
- For triangle OPT (where O is the center, P is one endpoint of the chord PQ, and T is the foot of the perpendicular from O to PQ):
OP2=OT2+PT2
102=H21+82
100=H21+64
H21=100−64=36⇒H1=6cm
OR2=OV2+RV2
102=H22+62
100=H22+36
H22=100−36=64⇒H2=8cm
- Since both chords are on the same side of the center:
Distance=H2−H1=8−6=2cm
- H1=6cm
- H2=8cm
- Since the chords are on opposite sides of the center:
Distance=H1+H2=6+8=14cm
- Distance when both chords are on the same side: 2 cm
- Distance when both chords are on opposite sides: 14 cm
Topper's Solved these Questions
Similar Questions
PQ and RS are two parallel chords of a circle whose centre is O and radius is 10 cm. If PQ=16 cm and RS=12 cm, find the distance between PQ and RS, if they lie: on the same side of centre O
View SolutionThe length of two parallel chords of a circle are 6 cm and 8 cm . The radius of the circle is 5 cm. Find the distance btween them if :
(i) chords are on the same side of the centre.
(ii) chords are on the opposite side of the centre.
View SolutionAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
View SolutionThe diameter of a circle is 20 cm. There are two parallel chords of length 16 cm . And 12 cm. Find the distance between these chords if chords are on the:
(i) same side
(ii) opposite side of the centre.
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ.
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
View SolutionAB and CD are two parallel chords of a circle with centre O such that AB=6 cm and CD=12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is (a)6 cm (b) 5 √2 cm (c) 7 cm (d) 3 √5 cm
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
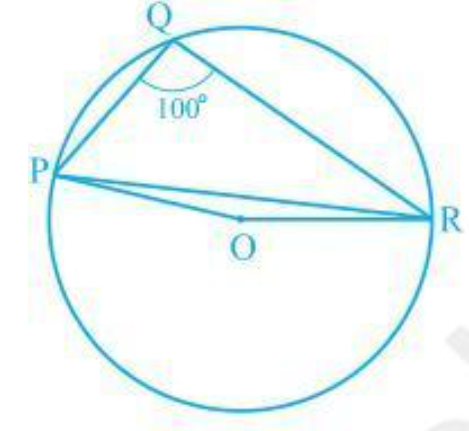
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13cm. A is any point on PQ. If PS=5cm, then find ar ( RAS)
View Solution

