The marks scored by 750 students in an examination are given in the form of a frequency distribution table.
.Marks 600−640,640−680,680−720and720−760,760−800,800−840,840−880
N⊙ofStudents:16451562841725918 Represent this data in the form of a histogram and construct a frequency polygon.
To solve the problem of representing the given data in the form of a histogram and constructing a frequency polygon, we will follow these steps:
Step 1: Create the Frequency Distribution Table
We have the following class intervals and frequencies:
| Marks | No. of Students |
|------------|-----------------|
| 600 - 640 | 16 |
| 640 - 680 | 45 |
| 680 - 720 | 156 |
| 720 - 760 | 284 |
| 760 - 800 | 172 |
| 800 - 840 | 59 |
| 840 - 880 | 18 |
Step 2: Set Up the Axes for the Histogram
- X-axis: Represents the marks (class intervals).
- Y-axis: Represents the number of students (frequency).
Step 3: Determine the Scale for the Axes
- For the X-axis, we can mark the class intervals: 600, 640, 680, 720, 760, 800, 840, 880.
- For the Y-axis, we can use a scale where each unit represents 20 students. Thus, we can mark the Y-axis from 0 to 300 in increments of 20.
Step 4: Plot the Histogram
1. For the class interval 600 - 640 with a frequency of 16, draw a bar from 600 to 640 that reaches up to 16 on the Y-axis.
2. For the class interval 640 - 680 with a frequency of 45, draw a bar from 640 to 680 that reaches up to 45 on the Y-axis.
3. For the class interval 680 - 720 with a frequency of 156, draw a bar from 680 to 720 that reaches up to 156 on the Y-axis.
4. For the class interval 720 - 760 with a frequency of 284, draw a bar from 720 to 760 that reaches up to 284 on the Y-axis.
5. For the class interval 760 - 800 with a frequency of 172, draw a bar from 760 to 800 that reaches up to 172 on the Y-axis.
6. For the class interval 800 - 840 with a frequency of 59, draw a bar from 800 to 840 that reaches up to 59 on the Y-axis.
7. For the class interval 840 - 880 with a frequency of 18, draw a bar from 840 to 880 that reaches up to 18 on the Y-axis.
Step 5: Construct the Frequency Polygon
1. Calculate the midpoints of each class interval:
- Midpoint of 600 - 640 = (600 + 640) / 2 = 620
- Midpoint of 640 - 680 = (640 + 680) / 2 = 660
- Midpoint of 680 - 720 = (680 + 720) / 2 = 700
- Midpoint of 720 - 760 = (720 + 760) / 2 = 740
- Midpoint of 760 - 800 = (760 + 800) / 2 = 780
- Midpoint of 800 - 840 = (800 + 840) / 2 = 820
- Midpoint of 840 - 880 = (840 + 880) / 2 = 860
2. Plot the midpoints against their corresponding frequencies:
- (620, 16)
- (660, 45)
- (700, 156)
- (740, 284)
- (780, 172)
- (820, 59)
- (860, 18)
3. Connect these points with straight lines to form the frequency polygon.
Final Step: Label the Graphs
- Label the histogram and the frequency polygon appropriately.
We have the following class intervals and frequencies:
|------------|-----------------|
| 600 - 640 | 16 |
| 640 - 680 | 45 |
| 680 - 720 | 156 |
| 720 - 760 | 284 |
| 760 - 800 | 172 |
| 800 - 840 | 59 |
| 840 - 880 | 18 |
- X-axis: Represents the marks (class intervals).
- Y-axis: Represents the number of students (frequency).
- For the X-axis, we can mark the class intervals: 600, 640, 680, 720, 760, 800, 840, 880.
- For the Y-axis, we can use a scale where each unit represents 20 students. Thus, we can mark the Y-axis from 0 to 300 in increments of 20.
1. For the class interval 600 - 640 with a frequency of 16, draw a bar from 600 to 640 that reaches up to 16 on the Y-axis.
2. For the class interval 640 - 680 with a frequency of 45, draw a bar from 640 to 680 that reaches up to 45 on the Y-axis.
3. For the class interval 680 - 720 with a frequency of 156, draw a bar from 680 to 720 that reaches up to 156 on the Y-axis.
4. For the class interval 720 - 760 with a frequency of 284, draw a bar from 720 to 760 that reaches up to 284 on the Y-axis.
5. For the class interval 760 - 800 with a frequency of 172, draw a bar from 760 to 800 that reaches up to 172 on the Y-axis.
6. For the class interval 800 - 840 with a frequency of 59, draw a bar from 800 to 840 that reaches up to 59 on the Y-axis.
7. For the class interval 840 - 880 with a frequency of 18, draw a bar from 840 to 880 that reaches up to 18 on the Y-axis.
1. Calculate the midpoints of each class interval:
- Midpoint of 600 - 640 = (600 + 640) / 2 = 620
- Midpoint of 640 - 680 = (640 + 680) / 2 = 660
- Midpoint of 680 - 720 = (680 + 720) / 2 = 700
- Midpoint of 720 - 760 = (720 + 760) / 2 = 740
- Midpoint of 760 - 800 = (760 + 800) / 2 = 780
- Midpoint of 800 - 840 = (800 + 840) / 2 = 820
- Midpoint of 840 - 880 = (840 + 880) / 2 = 860
- (620, 16)
- (660, 45)
- (700, 156)
- (740, 284)
- (780, 172)
- (820, 59)
- (860, 18)
- Label the histogram and the frequency polygon appropriately.
Topper's Solved these Questions
Similar Questions
The marks scored by 750 students in an examination are given in the form of a frequency distribution table: Marks No. of students Marks No. of students 600-640 16 760-800 172 640-680 45 800-840 59 680-720 156 840-880 18 720-760 284 Prepare a cumulative frequency table by less than method and draw an ogive.
View SolutionThe marks obtained by 32 students of a class are given below. Prepare a frequency table with class intervals 31−40,41−50,….. etc.
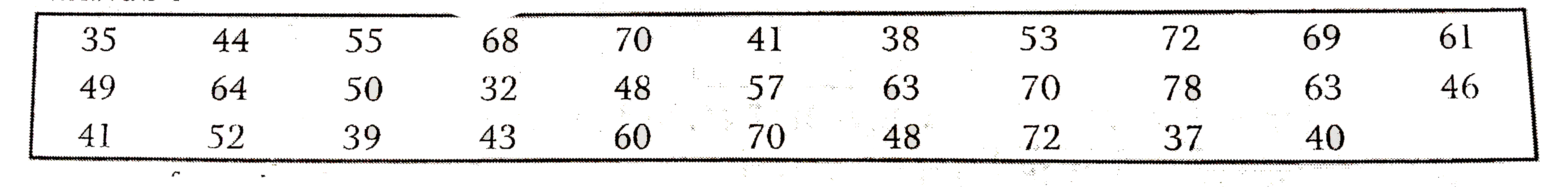
View SolutionThe marks distribution of 30 students m a mathematics examination are given in Table of Example 1. Find the mode of this data.
View SolutionFind the mode of the following frequency distribution of marks obtained by 50 students. Marks obtained 0−10 10−20 20−30 30−40 40−50 No. of students 5 12 20 10 3
View SolutionThe table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
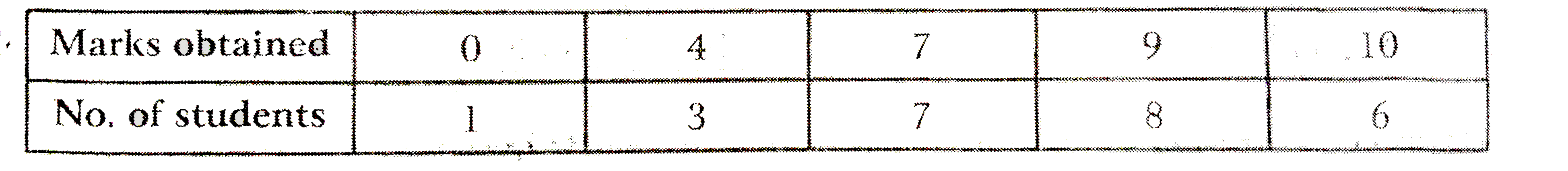
View SolutionFollowing are the marks obtained by 30 students in a examination

Taking class intervals 0−10,10−20,…..40−50 construct a frequency table.
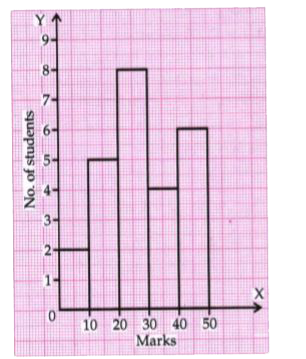
View SolutionThe historgam below represents the scores obtained by 25 students in a Mathematics mental test. Use the data to :
(i) Frame a frequency distribution table.
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View Solution
