In a certain city there are 30 colleges. Each college has 15 peons, 6 clerks, 1 typist and 1 section officer. Express the given information as a column matrix. Using scalar multiplication, find the total number of posts of each kind in all the colleges.
To solve the problem step by step, we will express the information given in the question as a column matrix and then use scalar multiplication to find the total number of posts of each kind in all the colleges.
Step 1: Define the column matrix for one college
We need to represent the number of each type of staff in one college as a column matrix.
The number of staff in one college is:
- Peons: 15
- Clerks: 6
- Typists: 1
- Section Officers: 1
Thus, we can define the column matrix X as follows:
X=⎡⎢
⎢
⎢⎣15611⎤⎥
⎥
⎥⎦
Step 2: Use scalar multiplication to find the total number of posts in 30 colleges
Since there are 30 colleges, we will multiply the column matrix X by the scalar 30.
30X=30×⎡⎢
⎢
⎢⎣15611⎤⎥
⎥
⎥⎦
Step 3: Perform the scalar multiplication
Now, we will multiply each element of the matrix X by 30:
30X=⎡⎢
⎢
⎢⎣30×1530×630×130×1⎤⎥
⎥
⎥⎦
Calculating each element:
1. 30×15=450
2. 30×6=180
3. 30×1=30
4. 30×1=30
Thus, we have:
30X=⎡⎢
⎢
⎢⎣4501803030⎤⎥
⎥
⎥⎦
Step 4: Interpret the results
The resulting column matrix represents the total number of posts of each kind in all 30 colleges:
- Total Peons: 450
- Total Clerks: 180
- Total Typists: 30
- Total Section Officers: 30
Final Result
The total number of posts of each kind in all the colleges is:
- Peons: 450
- Clerks: 180
- Typists: 30
- Section Officers: 30
---
We need to represent the number of each type of staff in one college as a column matrix.
- Peons: 15
- Clerks: 6
- Typists: 1
- Section Officers: 1
⎢
⎢⎣15611⎤⎥
⎥
⎥⎦
Since there are 30 colleges, we will multiply the column matrix X by the scalar 30.
⎢
⎢⎣15611⎤⎥
⎥
⎥⎦
Now, we will multiply each element of the matrix X by 30:
⎢
⎢⎣30×1530×630×130×1⎤⎥
⎥
⎥⎦
2. 30×6=180
3. 30×1=30
4. 30×1=30
⎢
⎢⎣4501803030⎤⎥
⎥
⎥⎦
The resulting column matrix represents the total number of posts of each kind in all 30 colleges:
- Total Clerks: 180
- Total Typists: 30
- Total Section Officers: 30
The total number of posts of each kind in all the colleges is:
- Peons: 450
- Clerks: 180
- Typists: 30
- Section Officers: 30
Topper's Solved these Questions
Similar Questions
A finance company has offices located in every division,
every district and every taluka in a certain state in India.
Assume that there are five divisions, thirty districts and
200 talukas in the state. Each office has one head clerk,
one cashier, one clerk and one peon. A divisional office
has, in addition, one office superintendent, two clerks,
one typist and one peon. A district office, has in
addition, one clerk and one peon. The basic monthly
salaries are as follows :
Office superintendent Rs 500, Head clerk Rs 200, cashier Rs 175, clerks and typist
Rs 150 and peon Rs 100. Using matrix notation find
The total number of posts of each kind in all the offices
taken together,View SolutionA finance company has offices located in ewery division,
every didtrict and every taluka in a certain state in India.
Assume that there are five divisions, thirty districts and
200 talukas in the state. Each office has one head clerk,
one cashier, one clerk and one peon. A divisional office
has, in addition, one office superntendent, two clerks,
one typist and one poen. A district office, has in
addition, one clerk and one peon. The basic monthly
salaries are as follows :
Office superintendernt Rs 500, Head clerk Rs 200, cashier Rs 175, clerks and typist
Rs 150 and peon Rs 100. Using matrix motation find
the total basic monthly salary bill of each kind of officeView Solution
Knowledge Check
- Question 1 - Select One
You Are Where You Say
Research on regional variations in English-language use has not only yielded answers to such life-altering questions a show people in different parts of the United States refer to carbonated beverages (“soda”? “pop”? “coke”?) it also illustrate show technology can change the very nature of research. While traditional, human-intensive data collection has all but disappeared in language studies, the explosion ofsocial media has open edne wave nues for investigation. [1] Perhaps the epitome of traditional methodology is the Dictionary of American Regional English, colloquially known as DARE. [2] Its fifth and final alphabetical volume—ending with “zydeco”— released in 2012, the dictionary represents decade so far duous work. [3] Overa six-year period from 1965 to 1970, university graduate students conducted inter views in morethan a thousand communities across the nation. [4] Their goal was to determine what names people used for such every day object sand concepts as a submarine sandwich.
(a “hero” in New York City but a “dagwood”in many parts of Minnesota, Iow a, and Colorado) and a heavy rainstorm(variously a “gullywasher,” “pour-down,” or “stumpmover”). [5] The work that dictionary founder Frederic G. Cassidy had expected to be finished by 1976 was not,in fact, completed in his life time. [6] The wait did not dampen enthusiasm among scholars. Scholars consider the work a signal achievement in linguistics. Not all research into regional English varieties requires such time, effort, and resources, however. Today’s researchers have foundth at the veritable army of trained volunteer straveling the country conducting face-to- face inter view scan sometimes be replaced by another army the vastarray of individuals volunteering details about their lives— and,in advertently, their language— through social media. Brice Russ of Ohio State University,for example, has employed software to sort through postings on one social media cite in search of particular words and phrases of interest as well as the location from which users are posting. From these data,
he was able, among other things, to confirm regional variations in people's terms for soft drinks. As the map shows. ,“soda” is comm only heard in the middle and western portions of the United States, “pop” is frequently used in many southern states, and “coke”ispre dominant in the north eastern and south west region sbutused else where as well. As interesting as Russ’s findings are, though, they’re true value lies in their reminder that the Internet is not merelya sophisticated tool for collecting data but is also itself a rich source of data
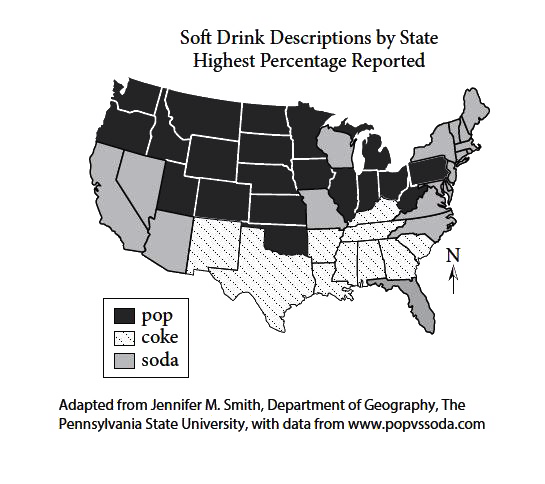
The writer wants the information in the passage to correspon as closely possible with the information in the map. Given that goaland assuming that there of the previous sentence would remain unchanged, in which sequence should the three terms for soft drinks be discussed?ANo ChangeB“pop,”“soda,”“coke”C“pop,”“coke,”“soda”D“soda,”“coke,”“pop”
A finance company has offices located in ewery division,
every didtrict and every taluka in a certain state in India.
Assume that there are five divisions, thirty districts and
200 talukas in the state. Each office has one head clerk,
one cashier, one clerk and one peon. A divisional office
has, in addition, one office superntendent, two clerks,
one typist and one poen. A district office, has in
addition, one clerk and one peon. The basic monthly
salaries are as follows :
Office superintendernt Rs 500, Head clerk Rs 200, cashier Rs 175, clerks and typist
Rs 150 and peon Rs 100. Using matrix motation find
the total basic monthly salary bill of all the offices taken
together.View SolutionA particular resistance wire has a resistance of 3.0 ohm per metre. Find :
The total resistance of three lengths of this wire each 1.5 m long, joined in parallel.View SolutionElementary Transformation of a matrix:
The following operation on a matrix are called elementary operations (transformations)
1. The interchange of any two rows (or columns)
2. The multiplication of the elements of any row (or column) by any nonzero number
3. The addition to the elements of any row (or column) the corresponding elements of any other row (or column) multiplied by any number
Echelon Form of matrix : A matrix A is said to be in echelon form if
(i) every row of A which has all its elements 0, occurs below row, which has a non-zero elements
(ii) the first non-zero element in each non –zero row is 1.
(iii) The number of zeros before the first non zero elements in a row is less than the number of such zeros in the next now.
[ A row of a matrix is said to be a zero row if all its elements are zero]
Note: Rank of a matrix does not change by application of any elementary operations
For example ⎡⎢⎣113012000⎤⎥⎦,⎡⎢⎣113601220000⎤⎥⎦ are echelon forms
The number of non-zero rows in the echelon form of a matrix is defined as its RANK. For example we can reduce the matrix A=⎡⎢⎣1232473610⎤⎥⎦ into echelon form using following elementary row transformation.
(i)R2→R2−2R1 and R3→R3−3R1⎡⎢⎣123001001⎤⎥⎦
(ii)R2→R2−2R1⎡⎢⎣123001000⎤⎥⎦
This is the echelon form of matrix A Number of nonzero rows in the echelon form =2 ⇒ Rank of the matrix A is 2
Rank of the matrix ⎡⎢⎣1111−1−1311⎤⎥⎦ is :View SolutionElementary Transformation of a matrix:
The following operation on a matrix are called elementary operations (transformations)
1. The interchange of any two rows (or columns)
2. The multiplication of the elements of any row (or column) by any nonzero number
3. The addition to the elements of any row (or column) the corresponding elements of any other row (or column) multiplied by any number
Echelon Form of matrix : A matrix A is said to be in echelon form if
(i) every row of A which has all its elements 0, occurs below row, which has a non-zero elements
(ii) the first non-zero element in each non –zero row is 1.
(iii) The number of zeros before the first non zero elements in a row is less than the number of such zeros in the next now.
[ A row of a matrix is said to be a zero row if all its elements are zero]
Note: Rank of a matrix does not change by application of any elementary operations
For example ⎡⎢⎣113012000⎤⎥⎦,⎡⎢⎣113601220000⎤⎥⎦ are echelon forms
The number of non-zero rows in the echelon form of a matrix is defined as its RANK. For example we can reduce the matrix A=⎡⎢⎣1232473610⎤⎥⎦ into echelon form using following elementary row transformation.
(i)R2→R2−2R1 and R3→R3−3R1⎡⎢⎣123001001⎤⎥⎦
(ii)R2→R2−2R1⎡⎢⎣123001000⎤⎥⎦
This is the echelon form of matrix A Number of nonzero rows in the echelon form =2 ⇒ Rank of the matrix A is 2
Rank of the matrix ⎡⎢⎣111−112443452⎤⎥⎦ is :View SolutionElementary Transformation of a matrix:
The following operation on a matrix are called elementary operations (transformations)
1. The interchange of any two rows (or columns)
2. The multiplication of the elements of any row (or column) by any nonzero number
3. The addition to the elements of any row (or column) the corresponding elements of any other row (or column) multiplied by any number
Echelon Form of matrix : A matrix A is said to be in echelon form if
(i) every row of A which has all its elements 0, occurs below row, which has a non-zero elements
(ii) the first non-zero element in each non –zero row is 1.
(iii) The number of zeros before the first non zero elements in a row is less than the number of such zeros in the next now.
[ A row of a matrix is said to be a zero row if all its elements are zero]
Note: Rank of a matrix does not change by application of any elementary operations
For example ⎡⎢⎣113012000⎤⎥⎦,⎡⎢⎣113601220000⎤⎥⎦ are echelon forms
The number of non-zero rows in the echelon form of a matrix is defined as its RANK. For example we can reduce the matrix A=⎡⎢⎣1232473610⎤⎥⎦ into echelon form using following elementary row transformation.
(i)R2→R2−2R1 and R3→R3−3R1⎡⎢⎣123001001⎤⎥⎦
(ii)R2→R2−2R1⎡⎢⎣123001000⎤⎥⎦
This is the echelon form of matrix A Number of nonzero rows in the echelon form =2 ⇒ Rank of the matrix A is 2
The echelon form of the matrix ⎡⎢⎣1343391291341⎤⎥⎦ is :View SolutionTwo mirros are inclinded by an angle 30∘. An object is placed 10∘ with the mirror M1. Find the positons of first two images formed by each mirror. Find the total number of images using (i) direct formula and (ii) counting the images.
View SolutionAn examination consists of 10 multiple choice questions, where each question has 4 options, only one of which is correct. In every question, a candidate earns 3 marks for choosing the correct opion, and -1 for choosing a wrong option. Assume that a candidate answers all questions by choosing exactly one option for each. Then find the number of distinct combinations of anwers which can earn the candidate a score from the set {15, 16,17,18, 19, 20}.
View Solution
