Question

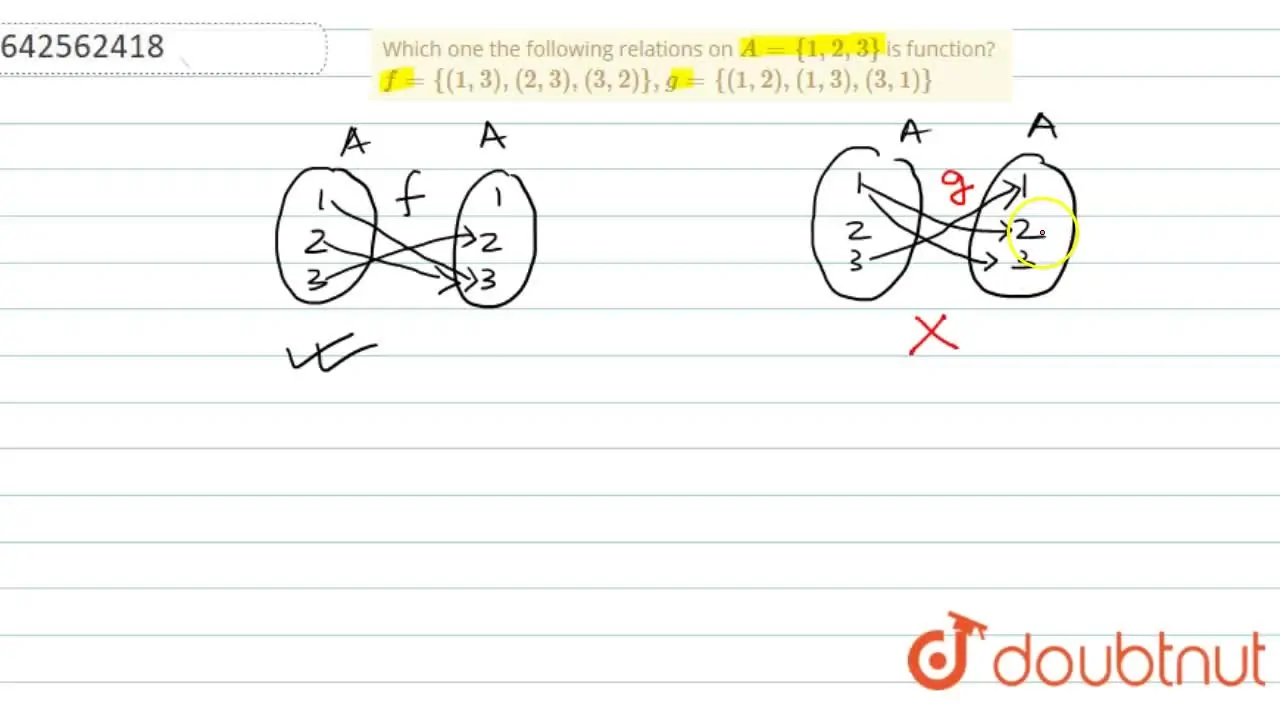
Which one the following relations on $A=\{1,2,3\}$
is function?
$f=\{(1,3),(2,3),(3,2)\},g=\{(1,2),(1,3),(3,1)\}$

Explanation

To determine which of the given relations on the set $$A=\{1,2,3\}$$ is a function, we need to analyze the two relations provided:

1. \( f = \{(1, 3), (2, 3), (3, 2)\} \)
2. \( g = \{(1, 2), (1, 3), (3, 1)\} \)

Step 1: Understand the definition of a function
A relation is a function if every element in the domain (the first component of each ordered pair) is associated with exactly one element in the codomain (the second component of each ordered pair).

Step 2: Analyze relation \( f \)
- The pairs in relation \( f \) are:
- \( 1 \to 3 \)
- \( 2 \to 3 \)
- \( 3 \to 2 \)

- Check the mapping:
- Element \( 1 \) maps to \( 3 \) (only one mapping)
- Element \( 2 \) maps to \( 3 \) (only one mapping)
- Element \( 3 \) maps to \( 2 \) (only one mapping)

Since each element in the domain \( \{1, 2, 3\} \) is associated with exactly one element in the codomain, relation \( f \) is a function.

Step 3: Analyze relation \( g \)
- The pairs in relation \( g \) are:
- \( 1 \to 2 \)
- \( 1 \to 3 \)
- \( 3 \to 1 \)

- Check the mapping:
- Element \( 1 \) maps to \( 2 \) and also to \( 3 \) (two mappings)
- Element \( 3 \) maps to \( 1 \) (only one mapping)
- Element \( 2 \) is not present in the domain, but it does not affect the function status.

Since element \( 1 \) is associated with two different elements in the codomain, relation \( g \) is not a function.

Conclusion
- Relation \( f \) is a function.
- Relation \( g \) is not a function.

Final Answer
The function among the given relations is \( f \).

---